2 一致推定量
この文書では、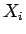 (
(
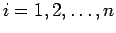 ) は、
ある一つの確率分布
) は、
ある一つの確率分布 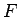 に従う、互いに独立な確率変数とする。
に従う、互いに独立な確率変数とする。
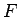 の (母) 平均 (
の (母) 平均 (![$=E[X_i]$](img7.gif) ) を
) を 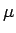 とし、
とし、
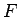 の (母) 分散 (
の (母) 分散 (![$=V[X_i]$](img9.gif) ) を
) を 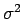 とする。
とする。
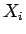 の 不偏分散
の 不偏分散 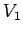 と 標本分散
と 標本分散 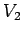 は、
次の式で定義される確率変数である。
は、
次の式で定義される確率変数である。
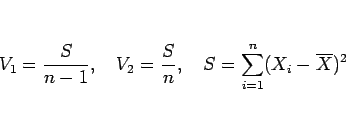 |
(1) |
ここで、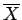 は
は 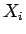 の算術平均 (確率変数としての平均ではない)
の算術平均 (確率変数としての平均ではない)
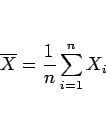
であり、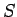 は平方和と呼ばれる。
は平方和と呼ばれる。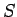 は、容易に次のように変形できる。
は、容易に次のように変形できる。
ここで、
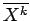 は、
は、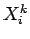 の算術平均を意味するものとする。
の算術平均を意味するものとする。
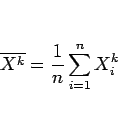
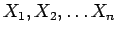 によって与えられるある確率変数
によって与えられるある確率変数
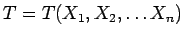 が、
が、
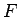 に関わるあるパラメータ
に関わるあるパラメータ 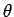 の 一致推定量 であるとは、
任意の正数
の 一致推定量 であるとは、
任意の正数 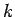 に対して、
に対して、
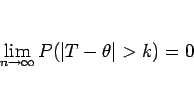 |
(3) |
となることを言うようである。
これは、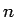 が十分大きければ、
が十分大きければ、
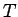 の値は
の値は 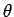 の近くに分布して、
の近くに分布して、
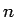 を大きくすれば、
を大きくすれば、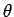 から離れた値を取る確率は
いくらでも小さくなる、ということを意味していて、
これにより
から離れた値を取る確率は
いくらでも小さくなる、ということを意味していて、
これにより 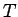 の値でパラメータ
の値でパラメータ 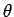 の値を推定 (点推定) できることの一つの保証が与えられることになる。
の値を推定 (点推定) できることの一つの保証が与えられることになる。
この一致性を示すのに重要なのが、次のチェビシェフの不等式である。
定理 1
確率変数 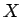 、および正数
、および正数 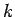 に対して、
に対して、
![\begin{displaymath}
P(\vert X-E[X]\vert>k)\leq \frac{V[X]}{k^2}
\end{displaymath}](img29.gif) |
(4) |
が成り立つ (![$E[X]$](img30.gif) は
は 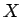 の平均、
の平均、![$V[X]$](img31.gif) は
は 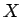 の分散)。
の分散)。
証明
分散 ![$V[X]$](img31.gif) を積分で表現して、
(4) の範囲に制限すれば、
を積分で表現して、
(4) の範囲に制限すれば、
![\begin{eqnarray*}V[X]
&=&
E[\vert X-E[X]\vert^2]
=
\int\vert X-E[X]\vert^2 d...
...\vert>k}\vert X-E[X]\vert^2 dP
\geq
k^2P(\vert X-E[X]\vert>k)
\end{eqnarray*}](img32.gif)
となるので、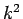 で両辺を割れば (4) が得られる。
で両辺を割れば (4) が得られる。
例えば、これを使って、標本平均 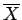 が
母平均
が
母平均 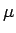 の一致推定量であることが確認してみよう。
の一致推定量であることが確認してみよう。
平均 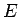 の線形性により、
の線形性により、
![\begin{displaymath}
E[\overline{X}]
=\frac{1}{n}\sum_{i=1}^nE[X_i]
=\frac{1}{n}\cdot n\mu
=\mu
\end{displaymath}](img35.gif)
であり、また、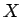 ,
, 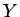 が独立の場合
が独立の場合
![$V[X+Y]=V[X]+V[Y]$](img37.gif) であるから、
であるから、
![\begin{displaymath}
V[\overline{X}]
=\frac{1}{n^2}\sum_{i=1}^nV[X_i]
=\frac{1}{n^2}\cdot n\sigma^2
=\frac{\sigma^2}{n}
\end{displaymath}](img38.gif)
となる。
よって、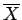 にチェビシェフの不等式を適用すると、
にチェビシェフの不等式を適用すると、
![\begin{displaymath}
P(\vert\overline{X}-\mu\vert>k)\leq \frac{V[\overline{X}]}{k...
...}
\rightarrow 0\hspace{1zw}(n\rightarrow\infty \mbox{ のとき})
\end{displaymath}](img39.gif)
となるので、
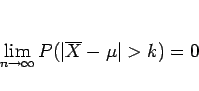
であることがわかり、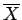 は
は 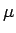 の一致推定量となる。
の一致推定量となる。
竹野茂治@新潟工科大学
2013年7月4日
![]() によって与えられるある確率変数
によって与えられるある確率変数
![]() が、
が、
![]() に関わるあるパラメータ
に関わるあるパラメータ ![]() の 一致推定量 であるとは、
任意の正数
の 一致推定量 であるとは、
任意の正数 ![]() に対して、
に対して、
![]() 、および正数
、および正数 ![]() に対して、
に対して、
![]() を積分で表現して、
(4) の範囲に制限すれば、
を積分で表現して、
(4) の範囲に制限すれば、
![]() が
母平均
が
母平均 ![]() の一致推定量であることが確認してみよう。
の一致推定量であることが確認してみよう。
![]() の線形性により、
の線形性により、