k ![]() 1
に対して
1
に対して
であるので、これをラプラス変換すると
(tksin t)' = ktk-1sin t + tkcos t
となる。この左辺は、(10) により、
[(tksin t)'] = k
[tk-1sin t] +
[tkcos t]
となるので、よって
[(tksin t)'] = s
[tksin t] - 0 = sFk
が成り立つ。同様に、
sFk = kFk-1 + Gk (k 1)
(10)
より、
(tkcos t)' = ktk-1cos t - tksin t
が成り立つので、(11), (12) より
sGk = kGk-1 - Fk (k 1)
(11)
となり、よって
= k
![$\displaystyle \left.\vphantom{\begin{array}{c}F_{k-1} G_{k-1}\end{array}}\right]$](img124.gif)
が得られる。今、 Uk = t(Fk, Gk) とし、右辺の行列を A とすると この行列は k にはよらず、
=
![$\displaystyle \left.\vphantom{\begin{array}{c}F_{k-1} G_{k-1}\end{array}}\right]$](img124.gif)
となるので、
Uk = AUk-1
(12)
となる。ここで、U0 は
Uk =AUk-1 =
A2Uk-2 = ... =
AkU0
なので、よって
U0 =![$\displaystyle \left.\vphantom{\begin{array}{c}1 s\end{array}}\right]$](img133.gif)
となり、この行列のベキを計算すれば Fk , Gk が求まることになる。 ただし、これもやはり順番に計算しないといけないので、 それほど楽ではない。
=
![$\displaystyle \left.\vphantom{\begin{array}{c}1 s\end{array}}\right]$](img133.gif)
(13)
とすれば、係数に k の含まれない漸化式
=
=
Uk
が得られる。ここで、いわゆるケーリー・ハミルントンの関係式より
= A
(k
1)
が成り立つので、k
A2 = (a + d )A - (ad - bc)E = 2sA - (s2 + 1)E
が得られる。 この最後の式は、行列計算を必要としない 3 項漸化式となっていて、
= A2
= 2sA
- (s2 +1)E
= 2s
- (s2 +1)
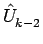
を意味する。この式と初期値
= 2s
- (s2 +1)
,
= 2s
- (s2 +1)
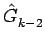
(14)
から順に
( ,
) = (1, s), (
,
) = (2s, s2 - 1)
(15)
| = | 2s |
||
| = | 2s |
||
| = | 2s |
||
| = | 2s |
||
| = | 2s(3s4 -10s2 + 3) |
となることになる。 ただし、(14) の行列計算と比べて、 それほど簡単であるともいい難い。
F5 ==
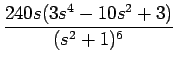
竹野茂治@新潟工科大学