7 節、9 節の議論により、
Fk
, Gk
の分子に表われる多項式 ![]() ,
, ![]() は
は
であることがわかる。 これは、3 項漸化式 (15) の、 初期値 (16) を満たす一般項でもある。
=
(s + i)k+1,
=
(s + i)k+1
(16)
(17) から、
![]() ,
, ![]() は一つおきの次数の項しか持たず、
よって必ず奇関数か偶関数のどちらかになることもすぐにわかる。
特に、次のことが言える:
は一つおきの次数の項しか持たず、
よって必ず奇関数か偶関数のどちらかになることもすぐにわかる。
特に、次のことが言える:
また、Fk , Gk の分子は (17) の定数倍であるから
そして、例えば F5
は、
| F5 | = | 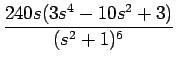 = = 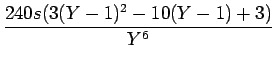 |
|
| = | 240s(3Y-4 -16Y-5 +16Y-6) | ||
| = | 240s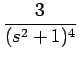 - - 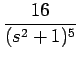 + + 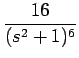 |
F2m-1 = s = s + ... +
,
F2m = = + ... +
,
G2m-1 = = + ... +
,
G2m = s = s + ... +
実際にこの係数を求めるのは容易ではないが、 これらをこの形に変形すること自体は意味があり、 有理関数のラプラス逆変換の計算に利用できる。 それについては、また別の機会にまとめる予定である。
竹野茂治@新潟工科大学