t5sin t = 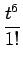 -
- 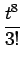 +
+ 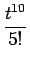 -
- 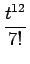 + ...
+ ...
より、
t5sin t =-
+
-
+ ...
| = | |||
| = | 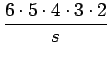 - - 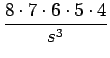 + + 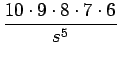 - ... - ... |
||
を 5 回微分したもの
= - 1 + X2 - X4 + X6 - X8 + ...
を使って表わされる。 しかし、左辺の 5 回の微分の計算は、 結局 6 節の t5 倍と見た場合の計算と 同じことをやらなければならないので、 ここから先の計算量はほぼその節の計算と同等である。
-= 6 . 5 . 4 . 3 . 2X - 8 . 7 . 6 . 5 . 4X3 + ...
竹野茂治@新潟工科大学