以後、
と書くことにする。
Fk(s) =[tksin t](s), Gk(s) =
[tkcos t](s)
まず、2 節の多項式倍の方法で考えると、
となるが、これは k が大きいと計算が大変である。
Fk = (- 1)k[sin t] = (- 1)k
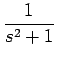
| F1 | = | - 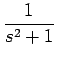 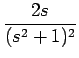 , , |
|
| F2 | = | (- 1)2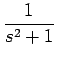 |
|
| = | -2(s2 +1)-2 -2s(- 2)(s2 +1)-3(2s) = - 2(s2 +1)-2 +8s2(s2 +1)-3 | ||
| = | - 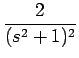 + + 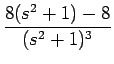 = = 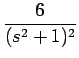 - - 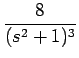 |
| F3 | = | - (F2)s = - (6Y-2 -8Y-3)s | |
| = | (12Y-3 -24Y-4)Ys = 24s(Y-3 -2Y-4), | ||
| F4 | = | - (F3)s = - {24s(Y-3 -2Y-4)}s | |
| = | -24(Y-3 -2Y-4) - 24s(- 3Y-4 +8Y-5)(2s) | ||
| = | 24(- Y-3 +2Y-4 +6s2Y-4 -16s2Y-5) | ||
| = | 24{ - Y-3 +2Y-4 +6(Y - 1)Y-4 -16(Y - 1)Y-5} | ||
| = | 24(5Y-3 -20Y-4 +16Y-5), | ||
| F5 | = | - (F4)s = - 24(5Y-3 -20Y-4 +16Y-5)s | |
| = | -24(- 15Y-4 +80Y-5 -80Y-6)(2s) | ||
| = | 240s(3Y-4 -16Y-5 +16Y-6) | ||
| = | 240s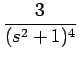 - - 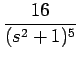 + + 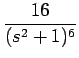 |
竹野茂治@新潟工科大学