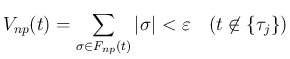 (90)
(90)
最終目標は、非物理 front の総量に対して、(7.78) の
とできることを示すことである。ここで、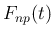 は、
すなわち
は、
すなわち  で存在する非物理 front 全体の集合とする。
で存在する非物理 front 全体の集合とする。
(90) を導くために、大きな世代に対する評価である
p142 の (7.75)、実際にはその改良版である (88), (89) を用いて評価する。
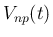 を、世代によって
を、世代によって
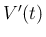 は、(89) より、
と評価でき、
は、(89) より、
と評価でき、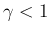 となるようにすれば、大きな
となるようにすれば、大きな 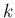 を取ることで
を取ることで 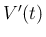 が十分小さくなることを示すことができる。
が十分小さくなることを示すことができる。
一方 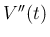 は、
は、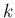 以下の世代の非物理 front の個数と、
その大きさの最大値 (43) との積で評価する。
以下の世代の非物理 front の個数と、
その大きさの最大値 (43) との積で評価する。
非物理 front の個数の評価を行うために、 またひとつ、[1] にはない新たな名前を導入する。 今まで「front 接続」という名前で、 ひとつの front をその特性族のまま最大に延長したものを考察してきたが、 これだと複数の front 接続が途中で合体 ([A-2],[S-2]) すると 1 本の front 接続になり、前方には一意に伸びるものの 後方には枝分かれする可能性があり、 また front 接続上で世代も変化しうる (前方に下がりうる) 可能性があった。 それらを排除するために、front 接続の枝葉を切り落として、 枝分かれのない 1 本の折れ線状の、世代も一定の「世代 front 接続」を 以下のように定義する。
世代 front 接続とは、front 接続同様に front を同じ特性族のもので 延長したものだが、
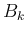 を世代が
を世代が 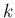 である世代 front 接続全体の集合とし、
である世代 front 接続全体の集合とし、
 は集合の要素の個数を意味する)。
また、初期階段関数
は集合の要素の個数を意味する)。
また、初期階段関数  の不連続点の個数を
の不連続点の個数を  とする。
とする。
第 1 世代の front は、 からのみ作られ、
からのみ作られ、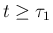 で新たに
作られることはないので、
で新たに
作られることはないので、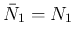 は、
は、
 から作られる front の総数に等しい。
よって、
から作られる front の総数に等しい。
よって、 の領域 (3.10 節の
の領域 (3.10 節の 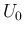 ) 内
にある Riemann 問題の初期値に対する最大の膨張波のサイズ
を
) 内
にある Riemann 問題の初期値に対する最大の膨張波のサイズ
を  とすると、
とすると、
 に対して、
に対して、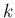 世代の front が新たに発生するのは
世代の front が新たに発生するのは
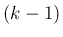 世代の front (世代 front 接続) と
世代の front (世代 front 接続) と 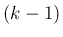 以下の front (世代 front 接続) との衝突であり、
1 組の世代 front 接続同士の衝突は高々 1 回しか起こり得ないので、
その衝突点の個数は
以下の front (世代 front 接続) との衝突であり、
1 組の世代 front 接続同士の衝突は高々 1 回しか起こり得ないので、
その衝突点の個数は
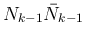 以下となる。
また、各衝突点では、
以下となる。
また、各衝突点では、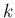 世代の front は流入 front とは
異なる特性族に出るので、その個数は
世代の front は流入 front とは
異なる特性族に出るので、その個数は
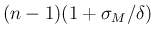 以下
となり、よって
以下
となり、よって  は、
は、
荒く評価すれば、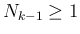 であれば、
であれば、
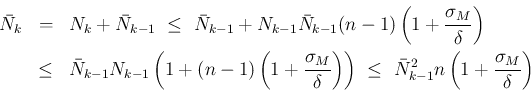
 ならば
ならば 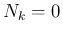 で、
よって
で、
よって
 となるから、当然この場合も
が成り立つ。
なお、衝突は有限回で終わるので、
となるから、当然この場合も
が成り立つ。
なお、衝突は有限回で終わるので、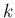 を大きくすれば、
あるところからは
を大きくすれば、
あるところからは 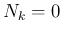 となることに注意する。
一般に、
となることに注意する。
一般に、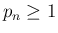 ,
,  に対して、
に対して、
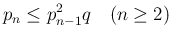

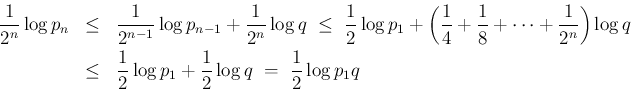

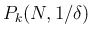 とすると、
とすると、
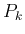 は
は 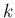 にしか依存しない
にしか依存しない  と
と 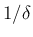 の多項式となる。
なお、[1] は、
の多項式となる。
なお、[1] は、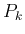 の具体的な形は紹介せず、
の具体的な形は紹介せず、
 と
と 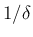 のなんらかの多項式で評価できる、
その式の表現は問題ではない、と述べている。
のなんらかの多項式で評価できる、
その式の表現は問題ではない、と述べている。
さて、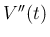 に戻れば、
に戻れば、 における
における 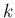 以下の世代の非物理 front の総数は、
以下の世代の非物理 front の総数は、
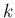 以下の世代の世代 front 接続の総数
以下の世代の世代 front 接続の総数 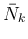 以下となるので、
(98)、および 5.2 節の (43) により、
以下となるので、
(98)、および 5.2 節の (43) により、
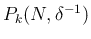 は
は 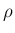 に依存しないから、
よって
に依存しないから、
よって 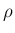 を小さくとることで、
を小さくとることで、
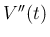 を十分小さく評価できることになる。
を十分小さく評価できることになる。
ここから (7.78) を導くのであるが、
これまででてきたパラメータ  ,
, 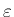 ,
,  ,
,
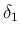 ,
, 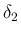 ,
, 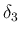 ,
, 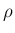 ,
, 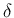 の意味と、
それらの依存関係について確認しておく。
の意味と、
それらの依存関係について確認しておく。
 は、初期階段関数
は、初期階段関数  の不連続点の個数で、[1] では
p127 (7.17) の下に現れる。これは、
の不連続点の個数で、[1] では
p127 (7.17) の下に現れる。これは、 の作り方により、
の作り方により、
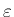 と初期値
と初期値 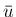 に依存して決まる値である。
に依存して決まる値である。
 は、定理 7.1 (p124) の (7.5), および定理 7.2 (p127) に
現れる正数で、初期値の全変動
は、定理 7.1 (p124) の (7.5), および定理 7.2 (p127) に
現れる正数で、初期値の全変動
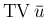 を上から押さえ、
これを十分小さく取ればこれらの定理が成り立つ、というもの。
よって、この
を上から押さえ、
これを十分小さく取ればこれらの定理が成り立つ、というもの。
よって、この  をどのように取ればよいか、
に答えることが最終目標となる。
をどのように取ればよいか、
に答えることが最終目標となる。
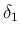 は、p133 に現れるもので、
Riemann 問題の解に対する評価である Lemma 7.2 を成り立たせるような
領域の大きさを意味し、本稿の
は、p133 に現れるもので、
Riemann 問題の解に対する評価である Lemma 7.2 を成り立たせるような
領域の大きさを意味し、本稿の 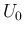 に対応する。
だから、ある程度は小さく取るものの、極限として 0 に近づけたり
するわけではない。
に対応する。
だから、ある程度は小さく取るものの、極限として 0 に近づけたり
するわけではない。
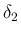 は、p131 に現れ、実際にはある条件 (本稿では (11) と、
3.10 節の
は、p131 に現れ、実際にはある条件 (本稿では (11) と、
3.10 節の 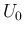 ,
, 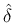 に
関する条件
に
関する条件
 ) を満たすパラメータであり、
その範囲内ではいくらでも小さく取ることができる。
) を満たすパラメータであり、
その範囲内ではいくらでも小さく取ることができる。
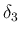 は、p138 に現れ、
は、p138 に現れ、
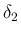 に対して本稿の (13) を満たすように
取る正数で、
に対して本稿の (13) を満たすように
取る正数で、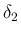 に依存して決まる値。
具体的には、(15) のように取ればよい。
初期階段関数の全変動がこの
に依存して決まる値。
具体的には、(15) のように取ればよい。
初期階段関数の全変動がこの 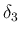 より
小さければ (本稿の (16))、
より
小さければ (本稿の (16))、
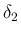 に対して (23) が成り立つことになる。
に対して (23) が成り立つことになる。
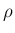 は、p132 の近似解の構成で現れる、
accurate method と simplified method の選択に使用される正数。
今のところは他とは独立に自由に選べる。
は、p132 の近似解の構成で現れる、
accurate method と simplified method の選択に使用される正数。
今のところは他とは独立に自由に選べる。
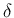 は、p129 の accurate method で
膨張波を膨張 front に分解するときに使われる正数。
これも今のところは他とは独立に選べる。
は、p129 の accurate method で
膨張波を膨張 front に分解するときに使われる正数。
これも今のところは他とは独立に選べる。
最終的に定理 7.2 の成立を示すためには、
最初に 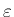 とは無関係に
とは無関係に 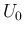 ([1] では
([1] では 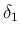 ) を
取り、それに対し、(11) と、
) を
取り、それに対し、(11) と、
 を満たし、
さらに (82) の
を満たし、
さらに (82) の 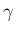 が
が 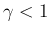 となるよう
となるよう
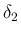 を 1 つ取り、
そして (13) を満たすように正数
を 1 つ取り、
そして (13) を満たすように正数 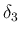 を 1 つ取る。
そして、正数
を 1 つ取る。
そして、正数  を、
を、
 となるように取る。
ここまでは
となるように取る。
ここまでは 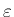 には依存しない。
には依存しない。
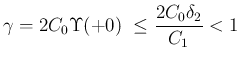
 であれば、(7.17) (p127) により
であれば、(7.17) (p127) により
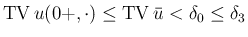
このとき、任意の正数 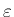 に対し、
に対し、
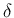 を、(38) を満たすように取る (
を、(38) を満たすように取る (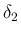 と
と 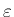 に依存)。
に依存)。

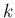 を取る (
を取る (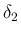 ,
, 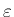 ,
, 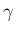 に依存)。
に依存)。
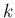 ,
,  ,
, 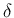 に対し、
に対し、
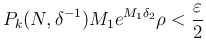
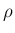 を取る (直接的には
を取る (直接的には 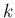 ,
,  ,
, 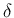 ,
, 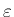 ,
, 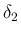 に依存)
に依存)
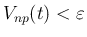 が得られる。
が得られる。
これで、「front の速度の変更部分を除いて」定理 7.2 が すべて検証できたことになる。
竹野茂治@新潟工科大学