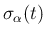 (
(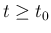 ) は、
新規には [S-1],[S-2] でのみ生成され、
無限に伸びる。
なお、
) は、
新規には [S-1],[S-2] でのみ生成され、
無限に伸びる。
なお、
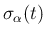 の符号は特に定められていないが、
本節では正として話を進めることにする。
の符号は特に定められていないが、
本節では正として話を進めることにする。
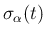 は、simplified method で作られるから、
その出発点
は、simplified method で作られるから、
その出発点 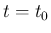 では、Lemma 7.2 (iii) より
では、Lemma 7.2 (iii) より
非物理 front 接続
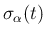 (
(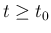 ) は、
新規には [S-1],[S-2] でのみ生成され、
無限に伸びる。
なお、
) は、
新規には [S-1],[S-2] でのみ生成され、
無限に伸びる。
なお、
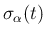 の符号は特に定められていないが、
本節では正として話を進めることにする。
の符号は特に定められていないが、
本節では正として話を進めることにする。
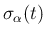 は、simplified method で作られるから、
その出発点
は、simplified method で作られるから、
その出発点 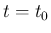 では、Lemma 7.2 (iii) より
では、Lemma 7.2 (iii) より
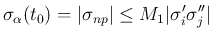
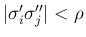 のときにしか実施しないので (p132)、
よって
である。
のときにしか実施しないので (p132)、
よって
である。
次は、衝突時刻 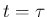 での評価を、
4 節同様 CASE 1 と CASE 2 に分けて考える。
での評価を、
4 節同様 CASE 1 と CASE 2 に分けて考える。
CASE 1 は
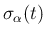 が他の front と衝突していない場合で、
この場合は当然
が他の front と衝突していない場合で、
この場合は当然
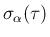 がその衝突点より左にあれば、
がその衝突点より左にあれば、
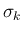 ,
, 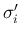 ,
,  のうちの物理 front はすべて
のうちの物理 front はすべて
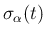 と approach し、
右にあれば衝突に関わるすべての front は
と approach し、
右にあれば衝突に関わるすべての front は
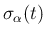 と approach しない。
と approach しない。
よって、[A-1] であれば、前者の場合は
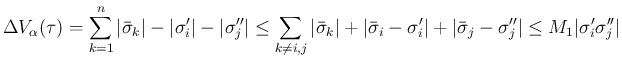
 となる。
[A-2] の場合も、
となる。
[A-2] の場合も、
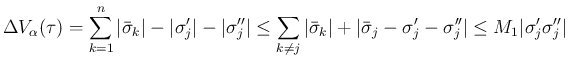
 となる。
[S-1] は、
となる。
[S-1] は、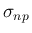 は
は
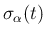 とは approach せず、
よって
とは approach せず、
よって
 。
[S-2] は、
。
[S-2] は、
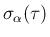 が衝突点の左ならば
が衝突点の左ならば
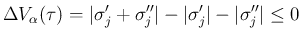
 。
[S-3] は
。
[S-3] は
 となる。
となる。
よって、すべて
 と
なるので、4.3 節の (31) と
同様にして (41) が得られる。
と
なるので、4.3 節の (31) と
同様にして (41) が得られる。
次は、CASE 2 の、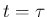 で
で
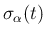 と
と 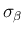 が衝突
する場合を考えてみる。この場合それは [S-3] となるので、
が衝突
する場合を考えてみる。この場合それは [S-3] となるので、
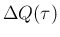 は、
(7), (11), (23) により、
は、
(7), (11), (23) により、

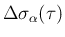 は、Lemma 7.2 (iv) より
は、Lemma 7.2 (iv) より

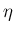 を定義すれば (34), (35) が得られ、よって (36) と
同様にして
を定義すれば (34), (35) が得られ、よって (36) と
同様にして

竹野茂治@新潟工科大学