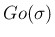 を作っている。
を作っている。
世代番号は、すべての front (各線分部分) に対して
あるレベル番号付けを行う規則であるが、
ID とは違い一意の番号をつけるわけではなく、
front から自然数への写像 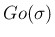 を作っている。
を作っている。
 に対する Riemann 問題の解から
作った front の世代番号は 1 とする
に対する Riemann 問題の解から
作った front の世代番号は 1 とする
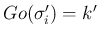 ,
,
 である front
である front 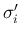 と
と  が衝突する場合、
が衝突する場合、
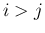 の場合 ([A-1],[S-1],[S-3])、
流入 front と同じ
の場合 ([A-1],[S-1],[S-3])、
流入 front と同じ 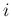 -特性族、
-特性族、 -特性族に出る front
-特性族に出る front
 ,
,
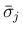 の世代番号は
の世代番号は
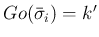 ,
,
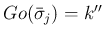 とし、
それ以外の特性族に出る front の世代番号は
すべて
とし、
それ以外の特性族に出る front の世代番号は
すべて
 とする
とする
 の場合 ([A-2],[S-2])、
流入 front と同じ
の場合 ([A-2],[S-2])、
流入 front と同じ  -特性族に出る front の世代番号は
-特性族に出る front の世代番号は
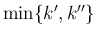 とし、
それ以外の特性族に出る front の世代番号は
すべて
とし、
それ以外の特性族に出る front の世代番号は
すべて
 とする
とする
そして、あらたに  ,
, 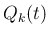 ,
,  (
(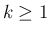 ) の記号を
導入している (p140)。
) の記号を
導入している (p140)。
 は、
は、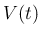 のうち、
のうち、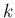 未満の世代の front をとりのぞいたもの、
未満の世代の front をとりのぞいたもの、
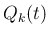 は、
は、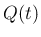 のうち、
のうち、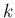 未満の世代同士の front の積の項を
とりのぞいたもの、
未満の世代同士の front の積の項を
とりのぞいたもの、 は衝突時刻
は衝突時刻 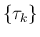 の集合を交わりのない
部分集合に分割したもの、となっている。
明らかに
の集合を交わりのない
部分集合に分割したもの、となっている。
明らかに 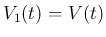 ,
, 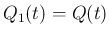 となる。
となる。
 は少しわかりにくいかもしれないが、
[1] の近似解の作り方の場合、各衝突時刻
は少しわかりにくいかもしれないが、
[1] の近似解の作り方の場合、各衝突時刻 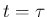 に対して、
その時刻に衝突する front
に対して、
その時刻に衝突する front 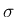 ,
,  の組が一意に決定し、
その両者の世代番号の大きい方を
の組が一意に決定し、
その両者の世代番号の大きい方を
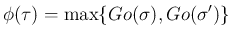
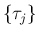 から自然数への写像となり、
それに対し
から自然数への写像となり、
それに対し
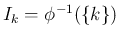 となる。
よって
となる。
よって  同士には交わりはなく、
同士には交わりはなく、

なお、[1] では、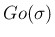 という関数は導入せず、
全 front に「
という関数は導入せず、
全 front に「 」という ID を示す添字をつけ、
」という ID を示す添字をつけ、
 の世代番号を
の世代番号を 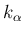 と書くことで
これらを定義しているが、その方法でも十分わかるし、
特にあいまいさがあるわけではない。
と書くことで
これらを定義しているが、その方法でも十分わかるし、
特にあいまいさがあるわけではない。
この 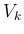 ,
, 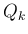 ,
,  に対し、p141 には次の 5 本の評価が上げられている。
に対し、p141 には次の 5 本の評価が上げられている。
 と
と 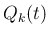 の、
衝突時刻での差分の場合分けによる評価であることに注意する。
の、
衝突時刻での差分の場合分けによる評価であることに注意する。
なお、1 本目の (47) はそれほど難しくはない。
 (
(
 ) より、
衝突する front の世代はいずれも
) より、
衝突する front の世代はいずれも 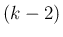 以下で、
よってその衝突で生成される front の世代もすべて
以下で、
よってその衝突で生成される front の世代もすべて 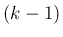 以下となり、
以下となり、
 にも
にも  にもそれらの front は含まれず、
よって (47) となる。
にもそれらの front は含まれず、
よって (47) となる。
以下、3 節同様、
その衝突時刻での流入 front を 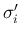 ,
,  (
(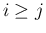 )、
その Riemann 問題の解を
)、
その Riemann 問題の解を
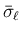 、
出力 front を
、
出力 front を  とし、
とし、
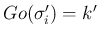 ,
,
 とする。
なお、
とする。
なお、
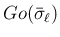 という記号も用いるが、
それは
という記号も用いるが、
それは
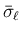 が膨張波である場合は、
その分解 front の (共通の) 世代番号とする。
が膨張波である場合は、
その分解 front の (共通の) 世代番号とする。