
 -特性族は真性非線形で、
-特性族は真性非線形で、
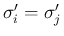 と
と  の少なくとも一方は負、
すなわち衝撃 front となる。
の少なくとも一方は負、
すなわち衝撃 front となる。
 であれば、
であれば、
 かどうかは、
かどうかは、
 かどうか、
および
かどうか、
および
 かどうかと一致するので
かどうかと一致するので
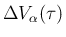 の
の  -特性族の項は
-特性族の項は
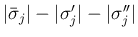 か 0 となる。
よっていずれの場合も
か 0 となる。
よっていずれの場合も
 の場合は、3.6 節と同じ 1. から 6. と同じ場合分けで考える。
なお、3.6 節で述べた通り、
の場合は、3.6 節と同じ 1. から 6. と同じ場合分けで考える。
なお、3.6 節で述べた通り、
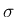 は十分小さいと見れば 2. の場合は起こらないとしてよいので、
2. を除外した 5 通りで考える。
は十分小さいと見れば 2. の場合は起こらないとしてよいので、
2. を除外した 5 通りで考える。
まず、1. の 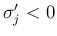 ,
, 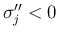 ,
,
 の
場合は
の
場合は
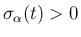 より
より
 ,
,
 ,
,
 で、
で、
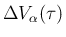 の
の  -特性族の項は
-特性族の項は
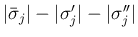 となるので、
(29) で評価される。
となるので、
(29) で評価される。
3. の 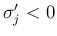 ,
, 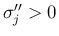 ,
,
 の場合は、
の場合は、
 ,
,
 だから
だから
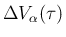 の
の  -特性族の項は
-特性族の項は
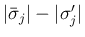 となるが、
となるが、

5. の 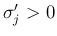 ,
, 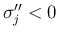 ,
,
 の場合は、
3. の
の場合は、
3. の 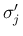 と
と  を入れ変えただけの形で同じ評価が
示される。
を入れ変えただけの形で同じ評価が
示される。
4. の 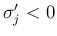 ,
, 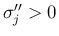 ,
,
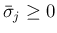 の場合は、
の場合は、
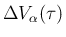 の
の  -特性族の項は
-特性族の項は 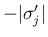 のみ
となるので、これも (29) で評価される。
のみ
となるので、これも (29) で評価される。
6. の 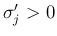 ,
, 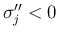 ,
,
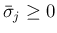 の場合も
4. の
の場合も
4. の 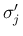 と
と  を入れ変えただけの形で同じ評価が
示される。
を入れ変えただけの形で同じ評価が
示される。
これで、[A-2] の場合はすべて (27) が 成り立つことがわかった。
竹野茂治@新潟工科大学