3.6
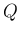 の評価: [A-2] の場合
の評価: [A-2] の場合
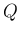 の評価: [A-2] の場合
の評価: [A-2] の場合
 -特性族が線形退化 (linearly degenerate) の場合を考えるが、
この場合
-特性族が線形退化 (linearly degenerate) の場合を考えるが、
この場合
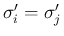 と
と  はどちらも
接触不連続 front であり、
その front 速度は
はどちらも
接触不連続 front であり、
その front 速度は
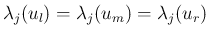 に
一致して、よって本来ならぶつからないはずである。
しかし、[1] の front tracking method では、
衝突時刻では必ず 2 つの front のみが衝突するよう、
必要なら front の速度を変更することを行う (p132 Remark 7.1) とあるので、
そのために隣り合う接触不連続 front がぶつかる可能性も否定できない。
よって一応それも考えておく。
に
一致して、よって本来ならぶつからないはずである。
しかし、[1] の front tracking method では、
衝突時刻では必ず 2 つの front のみが衝突するよう、
必要なら front の速度を変更することを行う (p132 Remark 7.1) とあるので、
そのために隣り合う接触不連続 front がぶつかる可能性も否定できない。
よって一応それも考えておく。
なお、Remark 7.1 は、3 つ以上の front が同じ衝突点で衝突しないように、 とだけ書いているが、実際には複数の衝突点の衝突時刻が一致してしまう 場合も避けていて、一つの衝突時刻では本当に 2 つの front のみが 衝突するようにしているようである。 詳しくは、6 で考察する。
この場合、その衝突後の Riemann 問題の解は当然単一の接触不連続波
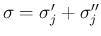 であり、この場合
であり、この場合
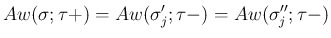
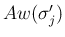 には
には  は含まれず、
は含まれず、
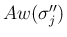 にも
にも 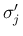 は含まれない。よって、
は含まれない。よって、
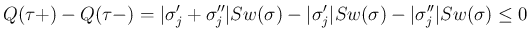
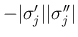 の項は得られない。
これは
の項は得られない。
これは 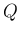 の approach する front 同士の項の中にこの接触不連続 front の
大きさの積
の approach する front 同士の項の中にこの接触不連続 front の
大きさの積
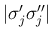 が存在しないからである。よって、
(7.56') をすべての衝突時刻
が存在しないからである。よって、
(7.56') をすべての衝突時刻 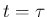 で成り立たせるためには、
この「同じ特性族の接触不連続 front同士の衝突」は起こらない
ようにしなければならない。
同様に、
で成り立たせるためには、
この「同じ特性族の接触不連続 front同士の衝突」は起こらない
ようにしなければならない。
同様に、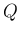 には存在しない、同じ特性族の膨張波の分解 front 同士の衝突も
起こらないようにしなければならない。
には存在しない、同じ特性族の膨張波の分解 front 同士の衝突も
起こらないようにしなければならない。
当然非物理 front も、その速度は 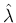 で固定されていて
勝手に変更できず、front 速度の変更には
これらのような制約がつくことになるが、
そういった速度の変更の制約に関して [1] には全く説明がない。
本当に速度の変更を行って問題なく近似解が構成できるかについては、
6 節で考察する。
で固定されていて
勝手に変更できず、front 速度の変更には
これらのような制約がつくことになるが、
そういった速度の変更の制約に関して [1] には全く説明がない。
本当に速度の変更を行って問題なく近似解が構成できるかについては、
6 節で考察する。
話を元に戻して、今度は accurate method で、 で、
で、
 -特性族が真性非線形 (genuinely nonlinear) の場合を考える。
-特性族が真性非線形 (genuinely nonlinear) の場合を考える。
この場合は、上に述べたように膨張波の分解 front 同士の衝突はないと考えれば、
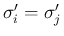 と
と  の少なくとも一方は衝撃 front で
負となる。当然
の少なくとも一方は衝撃 front で
負となる。当然
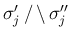 なので、
(3), (4) も成り立つ。
そして
なので、
(3), (4) も成り立つ。
そして 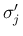 と
と  、および
、および
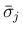 の
符号を考えると、その組み合わせは以下の 6 通りになる。
の
符号を考えると、その組み合わせは以下の 6 通りになる。
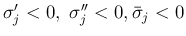 (いずれも衝撃 front)
(いずれも衝撃 front)
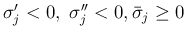 (生成される front のみ膨張 front)
(生成される front のみ膨張 front)
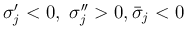 (右の流入 front のみ膨張 front)
(右の流入 front のみ膨張 front)
 (左の流入 front のみ衝撃 front)
(左の流入 front のみ衝撃 front)
 (左の流入 front のみ膨張 front)
(左の流入 front のみ膨張 front)
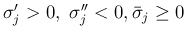 (右の流入 front のみ衝撃 front)
(右の流入 front のみ衝撃 front)


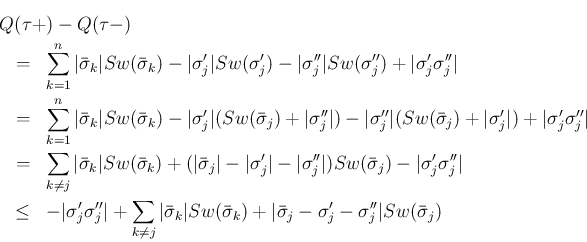
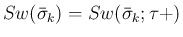 は
は
 を含まないから
を含まないから 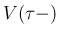 に含まれ、
よって Lemma 7.2 (ii) より
に含まれ、
よって Lemma 7.2 (ii) より
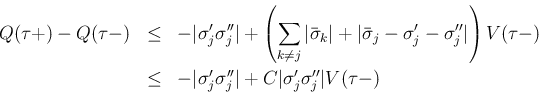
2. で
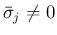 の場合は、
の場合は、


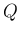 の差の、
の差の、
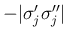 を除いた
を除いた  -特性族の front の部分の
-特性族の front の部分の
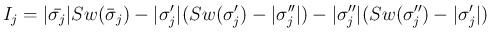

なお、この 2. は、Lemma 7.2 (ii) を考えれば 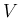 の場合と同様に
各
の場合と同様に
各 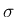 が十分小さいと仮定すれば
が十分小さいと仮定すれば
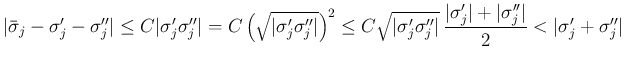
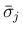 と
と
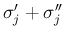 の符号が
同符号とできるので、2. 自体が起こらない、と見ることも可能である。
よって以後はそのように考えることにする。
の符号が
同符号とできるので、2. 自体が起こらない、と見ることも可能である。
よって以後はそのように考えることにする。
同様に、4. で
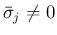 の場合は、
の場合は、
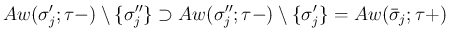
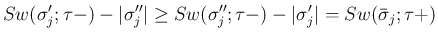
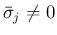 の場合も、
4. の
の場合も、
4. の 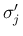 と
と  を入れかえたことと同等で、
を入れかえたことと同等で、



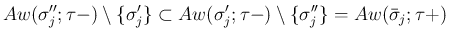
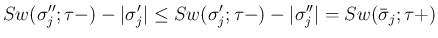
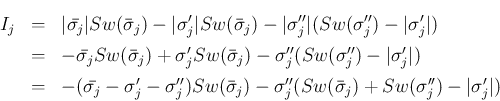
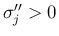 ,
,
 ,
,
 より
より
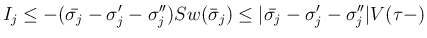
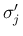 と
と  を
入れかえるだけなので、同様にして (7.56') が成立することがわかる。
を
入れかえるだけなので、同様にして (7.56') が成立することがわかる。
最後に、4., 6. (および 2.) の
 の場合であるが、
この場合は、
の場合であるが、
この場合は、 なので、(7.56') が得られることがわかる。
なので、(7.56') が得られることがわかる。
これで、accurate method の場合はすべて (7.56') が成り立つことが わかった。
竹野茂治@新潟工科大学