このオイラー座標系での理想気体の方程式系を
(4.1) の形に書いた場合、
この ![]() は特に
は特に
![\begin{displaymath}
F(U)=uU+G(U),\hspace{1zw}G(U)=\left[\begin{array}{c}0\\ P\\ Pu\end{array}\right]\end{displaymath}](img512.png)
今、解の不連続性がなめらか (![]() ) な曲線
) な曲線 ![]() に沿って
現れる (
に沿って
現れる (![]() 軸には平行には現れない) とし、
その不連続線以外では
軸には平行には現れない) とし、
その不連続線以外では ![]() はなめらか (
はなめらか (![]() ) な関数で
方程式 (4.1) を満たすとする。
そして、その不連続性は第一種の不連続、
すなわちこの不連続線へ向かっての
) な関数で
方程式 (4.1) を満たすとする。
そして、その不連続性は第一種の不連続、
すなわちこの不連続線へ向かっての ![]() の有限な極限が存在するとする。
なお、通常
の有限な極限が存在するとする。
なお、通常 ![]() 側の解を
側の解を ![]() ,
, ![]() 側の解を
側の解を ![]() のように
書くことが多く、ここでも適宜そのような記法を用いる。
のように
書くことが多く、ここでも適宜そのような記法を用いる。
物理的な要請とは、もちろん、
「保存量は、その不連続線の前後でも保存されること」である。
簡単のために、
![]() の近くを拡大して考えることで、
の近くを拡大して考えることで、
![]() を直線
を直線
![]() (
(![]() ) と見なし、
) と見なし、
![]() も
も ![]() の左右で定数ベクトル
の左右で定数ベクトル ![]() (
(
![]() ),
),
![]() (
(
![]() ) であると考える。
そして、
) であると考える。
そして、![]() を十分小さい定数として、
を十分小さい定数として、
![]() の時間変化での保存量の変化を考える。
の時間変化での保存量の変化を考える。
![]() ,
, ![]() を、それぞれ
を、それぞれ ![]() の左右の点とし、
の左右の点とし、
![]() でそれぞれの位置にあった気体の
でそれぞれの位置にあった気体の ![]() 秒後の位置を
それぞれ
秒後の位置を
それぞれ ![]() ,
, ![]() とし、
とし、
![]() とすると、
とすると、
このとき、![]() のときの
のときの
![]() における保存量
における保存量 ![]() と
と
![]() のときの
のときの
![]() における保存量
における保存量 ![]() の
値を比べると、
の
値を比べると、
![]() から
から ![]() への直線
への直線
![]() と
と
![]() から
から ![]() への直線
への直線
![]() は
流体とともに移動しているから、
これらの線を超えて流体の出入りはなく、よって保存量の出入り (
は
流体とともに移動しているから、
これらの線を超えて流体の出入りはなく、よって保存量の出入り (![]() ) もない。
よって、時間とともに境界に働く力によって増減される量 (
) もない。
よって、時間とともに境界に働く力によって増減される量 (![]() ) による
変化があるだけなので、
) による
変化があるだけなので、
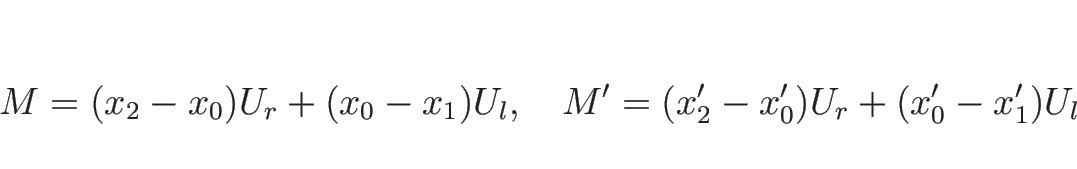
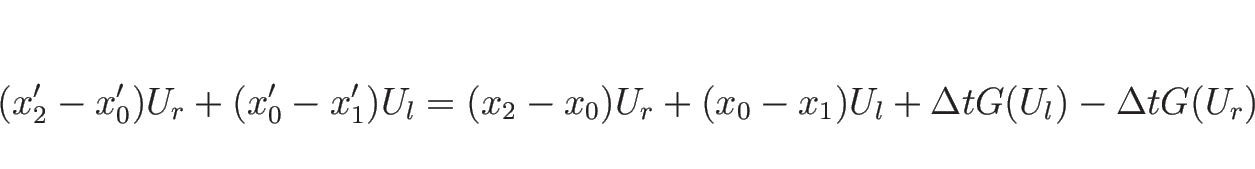
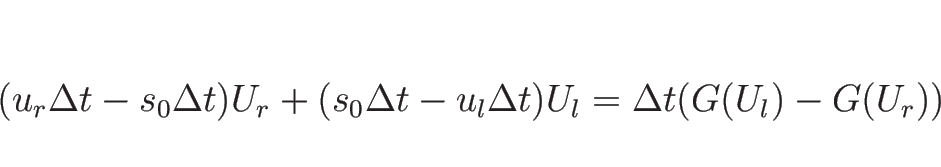
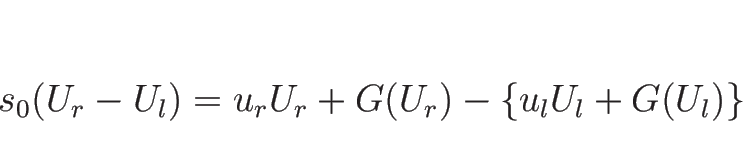
![\begin{displaymath}[g(U)]=\Bigl[g\Bigr]^{U=U_r}_{U=U_l}=g(U_r)-g(U_l)
\end{displaymath}](img551.png)
この (4.4) は不連続性の前後での ![]() の値と、
不連続線の伝播速度
の値と、
不連続線の伝播速度 ![]() が満たすべき関係式で、
ランキン-ユゴニオ関係式 (Rankine-Hugoniot relation)
または、ランキン-ユゴニオ条件 と呼ばれる。
が満たすべき関係式で、
ランキン-ユゴニオ関係式 (Rankine-Hugoniot relation)
または、ランキン-ユゴニオ条件 と呼ばれる。
上の議論は、![]() の付近で拡大して定数と見る、
ということをしなくても同じことを行うことは可能である。
の付近で拡大して定数と見る、
ということをしなくても同じことを行うことは可能である。
![]() で不連続線の
で不連続線の ![]() の
左側に曲線
の
左側に曲線 ![]() があるように
があるように ![]() を取り、
右側に曲線
を取り、
右側に曲線 ![]() があるように
があるように ![]() を取る。
そして、
を取る。
そして、![]() をこの不連続線の左側の領域、
をこの不連続線の左側の領域、![]() を右側の領域とする:
を右側の領域とする:
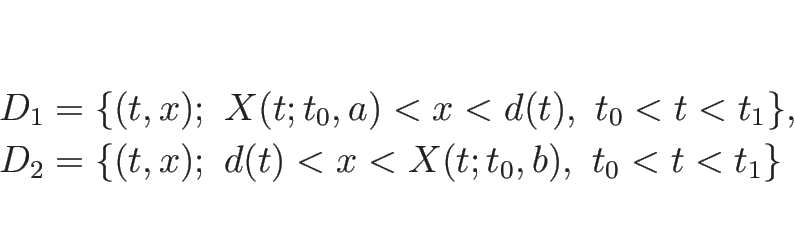
このとき上の考察と同様に、曲線 ![]() ,
, ![]() を超えて
保存量の流入、流出はなく、その上での
を超えて
保存量の流入、流出はなく、その上での ![]() による影響があるだけなので、
による影響があるだけなので、
![]() の内部では
の内部では ![]() を満たし、
かつ
を満たし、
かつ ![]() の
の ![]() への極限は存在するのでそれを
への極限は存在するのでそれを ![]() と書けば、
Green の公式:
と書けば、
Green の公式:
![\begin{eqnarray*}0
&=&
-\int_a^bU(t_0,x)dx + \int_{X_1}^{X_2}U(t_1,x)dx
+\int...
...}^{t_1}\Bigl[F(U(t,x))-d'(t)U(t,x)\Bigr]^{x=d(t)+0}_{x=d(t)-0}dt \end{eqnarray*}](img574.png)
(4.5) により、
この式の右辺の最初の 3 項の和は 0 であるから、
![]() の両端の値での積分のみが残り、
の両端の値での積分のみが残り、
![\begin{displaymath}
\int_{t_0}^{t_1}\Bigl[F(U(t,x))-d'(t)U(t,x)\Bigr]^{x=d(t)+0}_{x=d(t)-0}dt=0
\end{displaymath}](img575.png)
竹野茂治@新潟工科大学