リーマン不変量は、3.4 節で見たように
各特性方向に ![]() 個存在するので、
個存在するので、
![]() の場合は 1-リーマン不変量が 1 つ、
2-リーマン不変量が 1 つあるだけである。
これらをそれぞれ
の場合は 1-リーマン不変量が 1 つ、
2-リーマン不変量が 1 つあるだけである。
これらをそれぞれ ![]() ,
, ![]() とすると、
とすると、
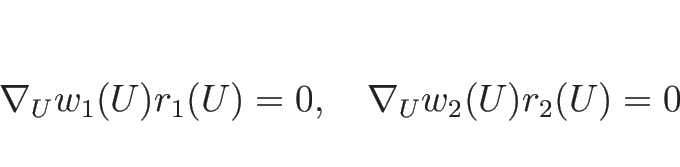
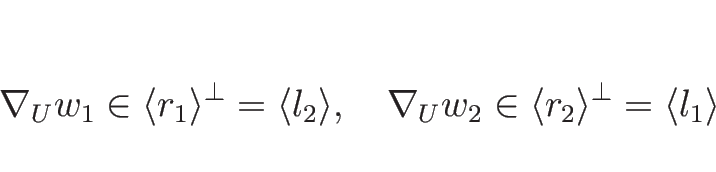
例えばバロトロピックのオイラー座標系の場合は、
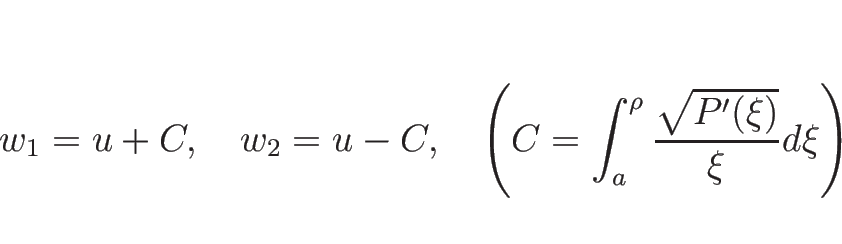
![]() なので、
なので、
![]() が滑らかならば、方程式
が滑らかならば、方程式
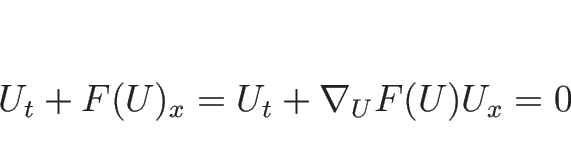
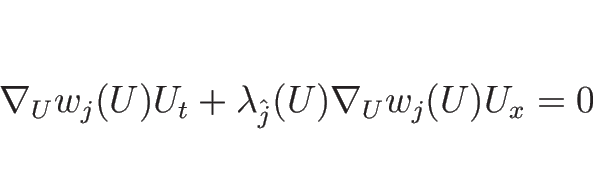
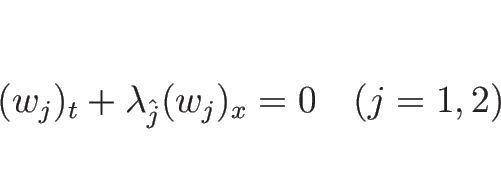
![\begin{displaymath}
\left[\begin{array}{c}w_1\\ w_2\end{array}\right]_t+
\left[\...
...\right]
\left[\begin{array}{c}w_1\\ w_2\end{array}\right]_x
=0
\end{displaymath}](img1199.png)
さて、相空間を ![]() を座標系として見るとすると、
を座標系として見るとすると、
![]() は
は ![]() の積分曲線上一定なので、
相空間上の膨張波曲線
の積分曲線上一定なので、
相空間上の膨張波曲線 ![]() と接触不連続曲線
と接触不連続曲線 ![]() は
この空間 (平面) 上では
は
この空間 (平面) 上では ![]() 軸に垂直
(
軸に垂直
(![]() 軸に平行) な半直線、または直線となって
見やすくなる。
しかも、必要なら
軸に平行) な半直線、または直線となって
見やすくなる。
しかも、必要なら ![]() を
を ![]() 倍しておいて、
倍しておいて、
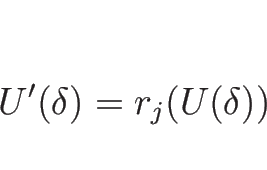
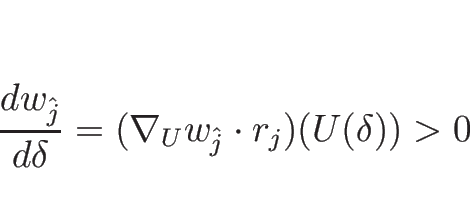
バロトロピックのオイラー座標系の方程式の場合は、
![\begin{eqnarray*}\nabla_U w_1\cdot r_2
&=& (C_\rho,1)\left[\begin{array}{c}\rho...
...begin{array}{c}-\rho \\ \sqrt{P'}\end{array}\right]=2\sqrt{P'}>0,\end{eqnarray*}](img1208.png)
ただし、この場合、積分
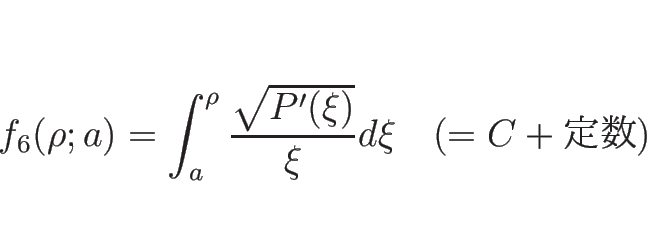
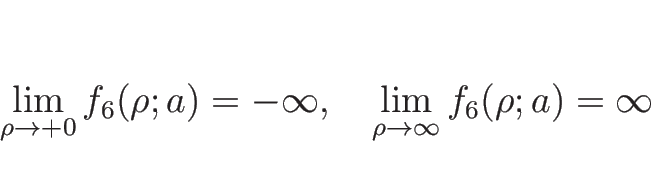
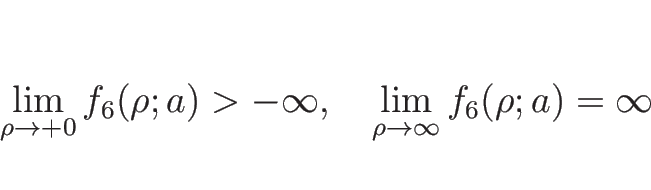
さらに
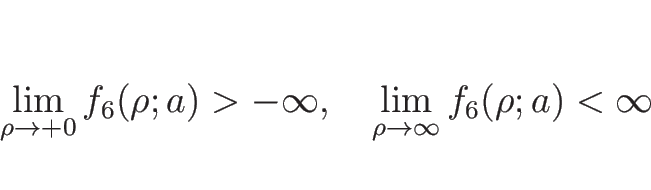
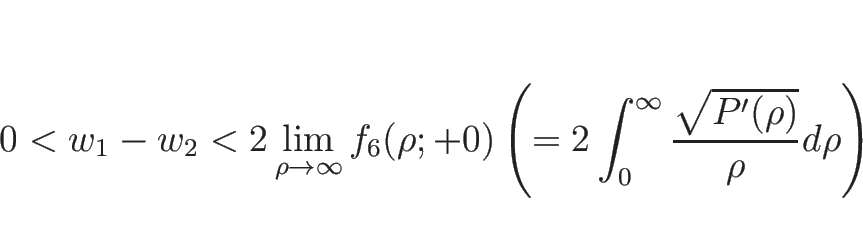
次は、バロトロピックのオイラー座標系の場合の、
![]() 平面での衝撃波曲線
平面での衝撃波曲線 ![]() (および
(および
![]() )
を考えてみる。
)
を考えてみる。
これらは、5.7 節で見たように、
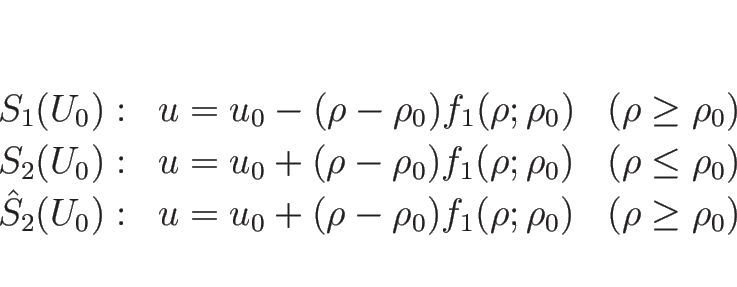
![]() は、
は、![]() 平面では
平面では ![]() をパラメータとして
をパラメータとして
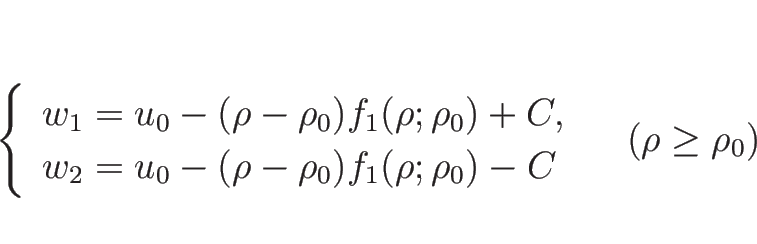
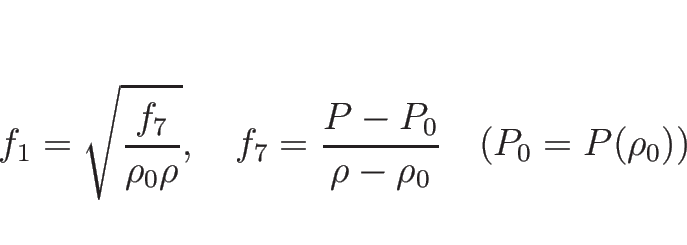
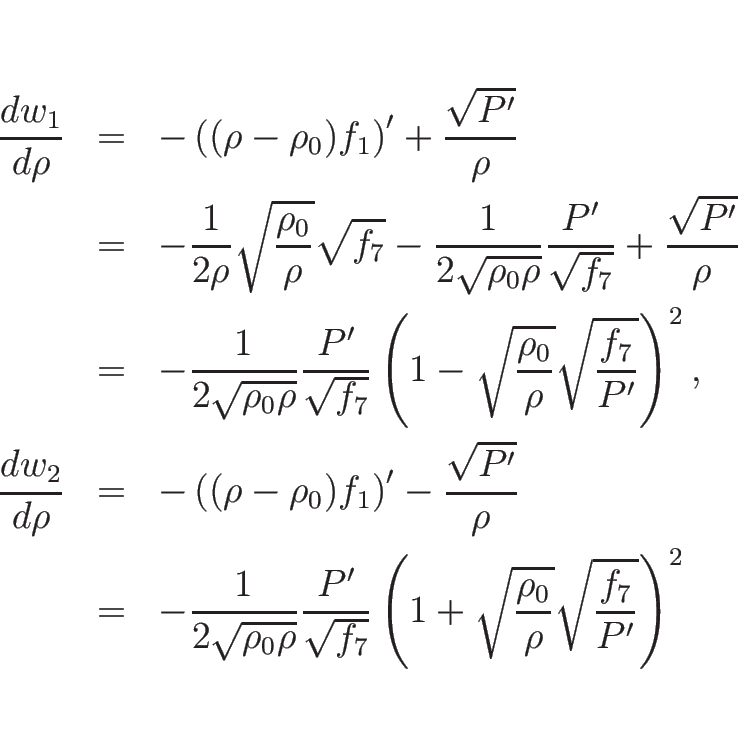
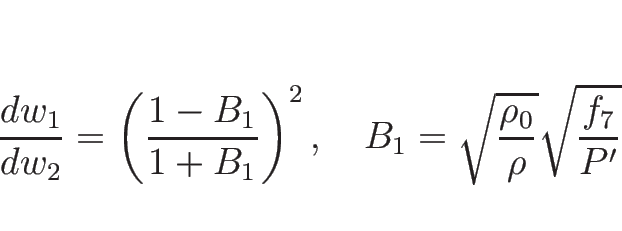
同様に、![]() の場合は、
の場合は、
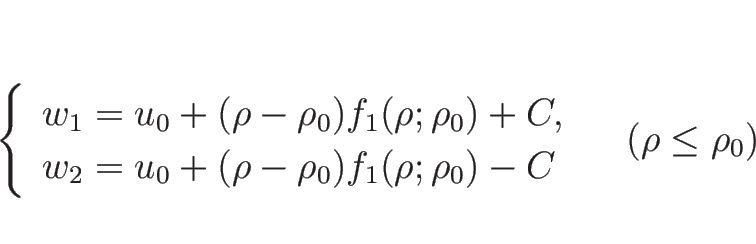
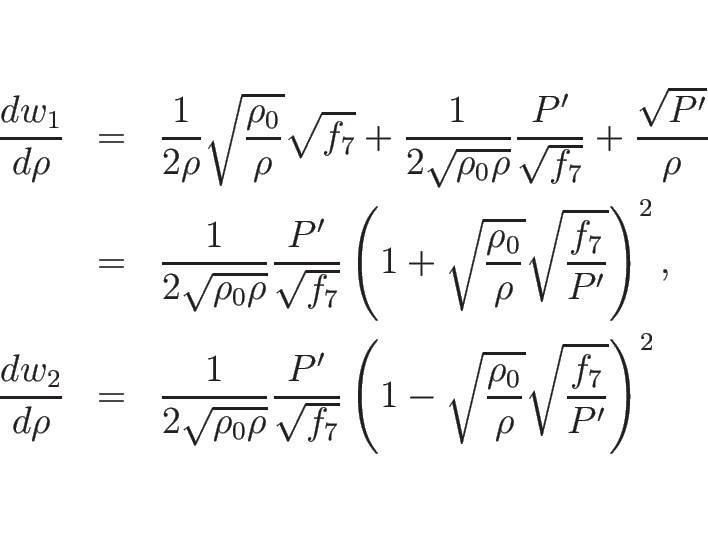
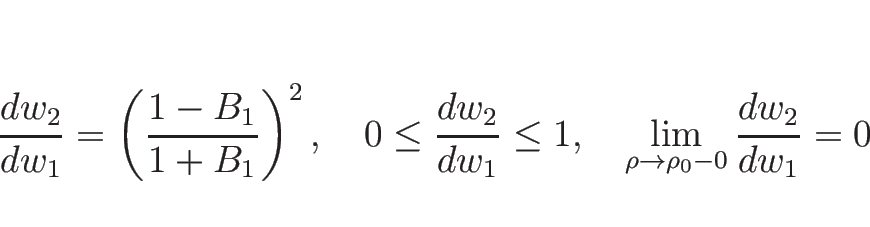
この場合、そのリーマン問題の解に表われる波は、
![]() ,
, ![]() の位置関係により変わるが、
図 5.12 のように
の位置関係により変わるが、
図 5.12 のように ![]() を中心に
を中心に
![]() ,
, ![]() を書いたときにそれらにより分割される
4 つの領域のどこに
を書いたときにそれらにより分割される
4 つの領域のどこに ![]() があるかによって
その波の表われ方が決まる。
があるかによって
その波の表われ方が決まる。
![]() が図 5.12 の領域 I に入る場合は、
1-膨張波曲線 (
が図 5.12 の領域 I に入る場合は、
1-膨張波曲線 (![]() ) と 2-膨張波曲線 (
) と 2-膨張波曲線 (![]() ) によって
) によって
![]() と
と ![]() がつながるので、
がつながるので、![]() と
と ![]() をつなぐ 1-膨張波、
をつなぐ 1-膨張波、
![]() と
と ![]() をつなぐ 2-膨張波によって
リーマン問題の解が構成される (図 5.13)。
この
をつなぐ 2-膨張波によって
リーマン問題の解が構成される (図 5.13)。
この ![]() は
は ![]() と
と
![]() の交点と見ることもできる。
の交点と見ることもできる。
![]() が図 5.12 の領域 II に入るときは、
が図 5.12 の領域 II に入るときは、
![]() と
と
![]() が (
が (![]() で) 交わるので、
で) 交わるので、
![]() と
と ![]() により
により ![]() と
と ![]() がつながる。
よって、
がつながる。
よって、![]() と
と ![]() は 1-衝撃波、
は 1-衝撃波、
![]() と
と ![]() は 2-膨張波でつながり、
それがリーマン問題の解となる (図 5.14)。
は 2-膨張波でつながり、
それがリーマン問題の解となる (図 5.14)。
![]() が図 5.12 の領域 III に入るときは、
が図 5.12 の領域 III に入るときは、
![]() と
と
![]() が交わるので、
1-衝撃波と 2-膨張波でリーマン問題の解が作られる
(図 5.15)。
が交わるので、
1-衝撃波と 2-膨張波でリーマン問題の解が作られる
(図 5.15)。
![]() が図 5.12 の領域 IV に入るときは、
が図 5.12 の領域 IV に入るときは、
![]() と
と
![]() が交わるので、
1-衝撃波と 2-膨張波が現われることになる
(図 5.16)。
が交わるので、
1-衝撃波と 2-膨張波が現われることになる
(図 5.16)。
なお、
![]() (
(![]() ) のように、
) のように、
![]() が平面全体でない場合
(図 5.9 参照)
は、
図 5.17 のように
が平面全体でない場合
(図 5.9 参照)
は、
図 5.17 のように
![]() は有限のところで
は有限のところで ![]() の境界にぶつかるので、
V の領域に
の境界にぶつかるので、
V の領域に ![]() が入る場合、すなわち
が入る場合、すなわち
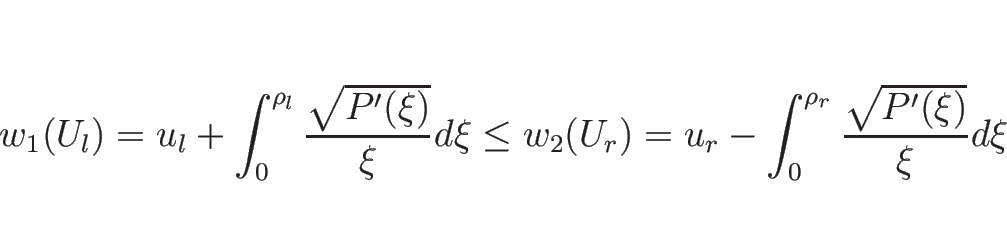
竹野茂治@新潟工科大学