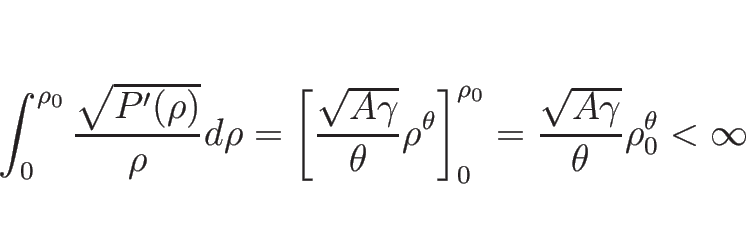5.7 バロトロピックのオイラー座標系の場合
バロトロピックのオイラー座標系の場合、
3.7 節、
4.10 節で見たように 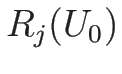 ,
, 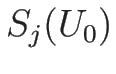 (
(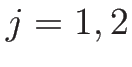 ) は以下のように表される。
) は以下のように表される。
よって、
とすれば、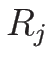 ,
, 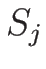 をつないだ
をつないだ 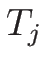 は
は
となる。この場合、
であるので、
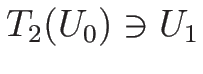 を逆に
を逆に 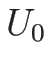 について解いた
について解いた
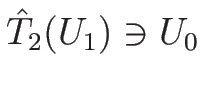 を考えると、
を考えると、
となることがわかる。
リーマン問題の解は、
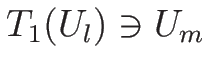 ,
,
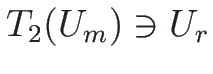 となる
となる
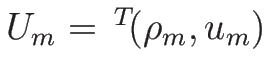 を求めればよいが、
それは
を求めればよいが、
それは 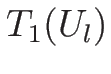 と
と
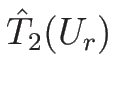 の交点として
の交点として
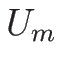 を求めればよいことになる。
それにより、
を求めればよいことになる。
それにより、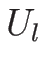 と
と 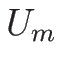 を結ぶ 1-単純波、
を結ぶ 1-単純波、
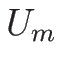 と
と 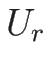 を結ぶ 2-単純波によって
リーマン問題の解が構成される。
を結ぶ 2-単純波によって
リーマン問題の解が構成される。
これが常に解けるかどうかを考えてみる。
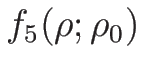 は、
は、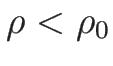 ならば
ならば
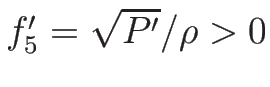 であり、
であり、
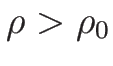 ならば
ならば
であり、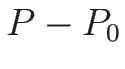 ,
,
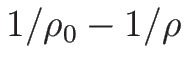 は
は 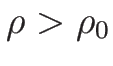 ではいずれも正で、
かつ増加関数なので
ではいずれも正で、
かつ増加関数なので 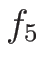 (
( ) も増加関数となる。
) も増加関数となる。
よって、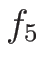 はすべての
はすべての 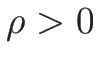 に対して増加関数であり、
に対して増加関数であり、
となるので、交点を求める方程式
を
と書き直せば、この左辺は 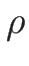 の増加関数で、
の増加関数で、
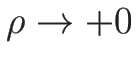 のときは
のときは
となり、
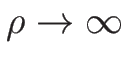 のときは
のときは
となるので、解が 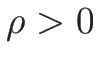 で求まるためには
で求まるためには
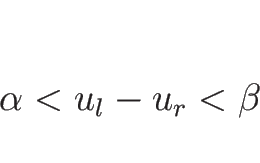 |
(5.114) |
であることが条件となる。
例えば 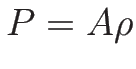 のときは
のときは
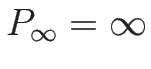 ,
,
なので、この条件 (5.6) は常に満たされ、
よってどんな 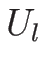 ,
, 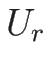 に対しても解が求まる。
一方
に対しても解が求まる。
一方
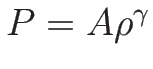 (
(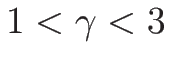 ) の場合は、
) の場合は、
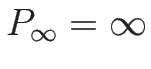 であるが、
であるが、
なので、(5.6) は
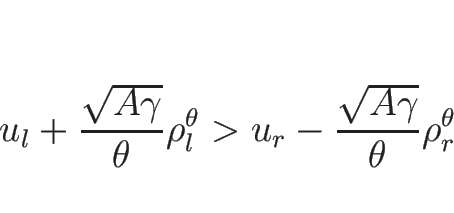 |
(5.115) |
となり、これが満たされるときのみ解を持つことになる。
竹野茂治@新潟工科大学
2018-08-01
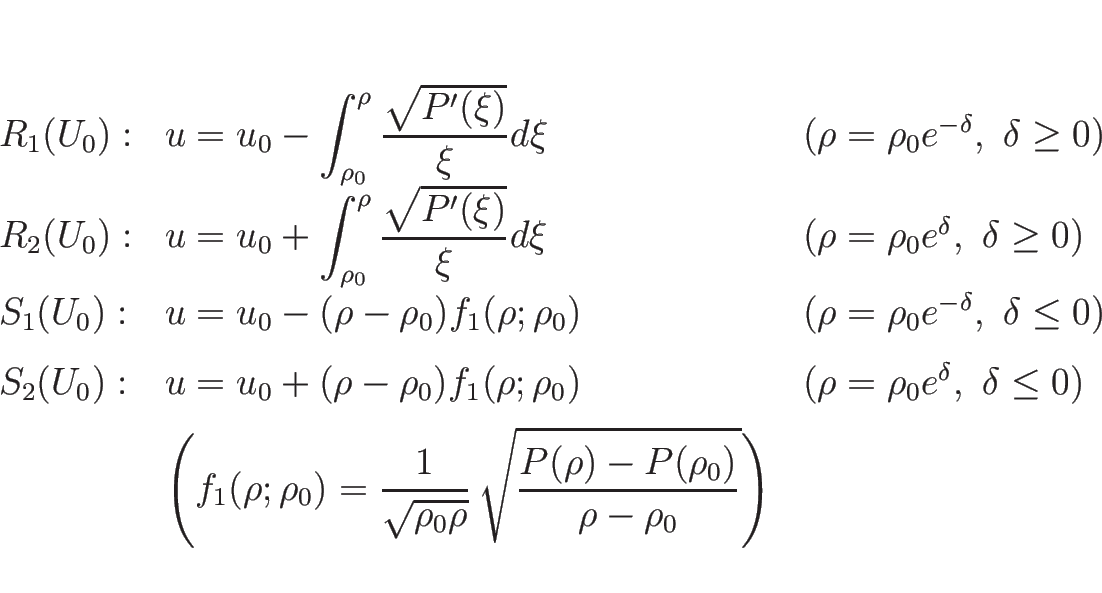
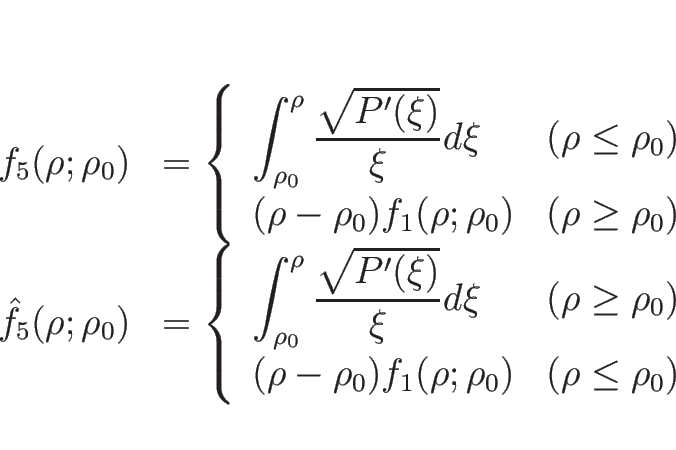
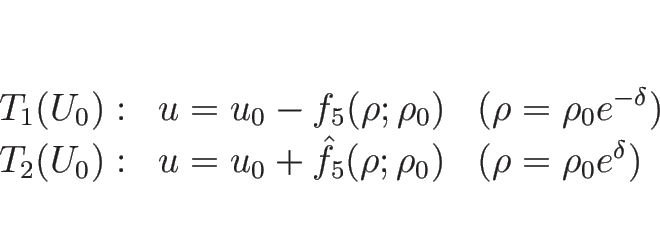
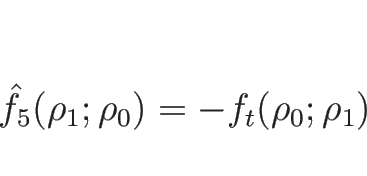
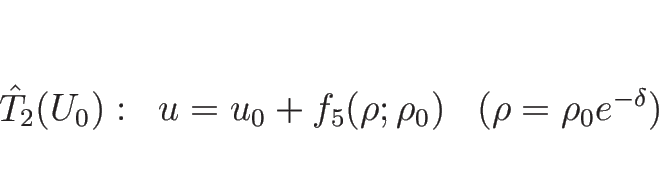
![]() ,
,
![]() となる
となる
![]() を求めればよいが、
それは
を求めればよいが、
それは ![]() と
と
![]() の交点として
の交点として
![]() を求めればよいことになる。
それにより、
を求めればよいことになる。
それにより、![]() と
と ![]() を結ぶ 1-単純波、
を結ぶ 1-単純波、
![]() と
と ![]() を結ぶ 2-単純波によって
リーマン問題の解が構成される。
を結ぶ 2-単純波によって
リーマン問題の解が構成される。
![]() は、
は、![]() ならば
ならば
![]() であり、
であり、
![]() ならば
ならば
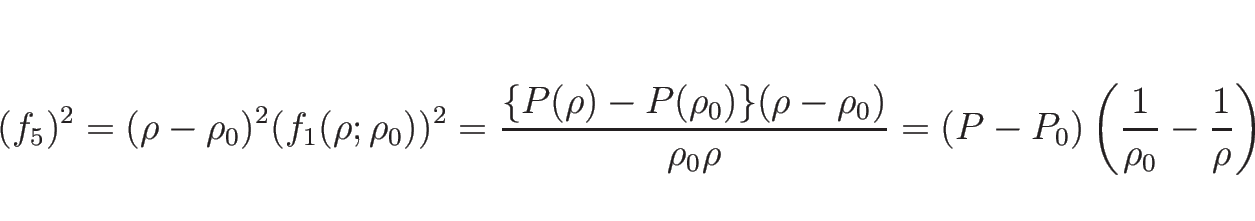
![]() はすべての
はすべての ![]() に対して増加関数であり、
に対して増加関数であり、
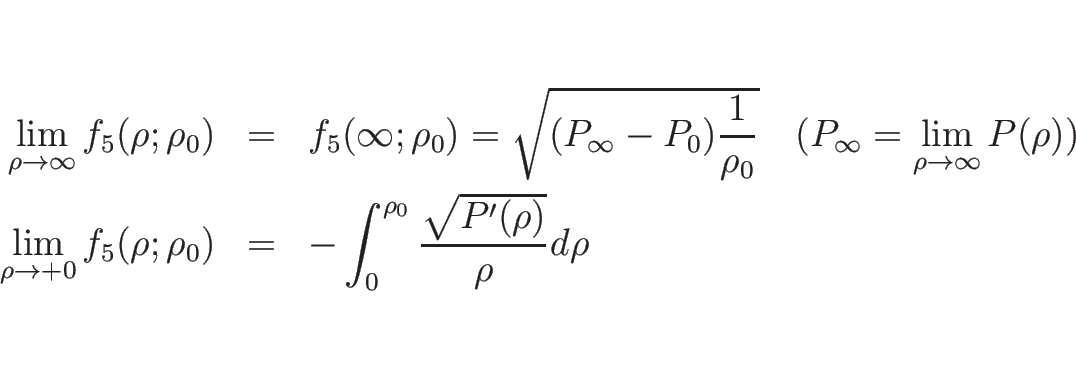
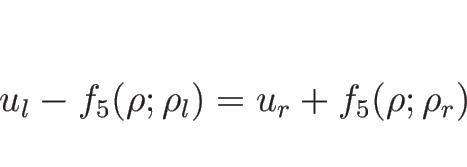
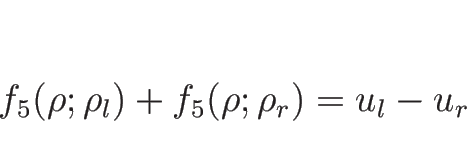
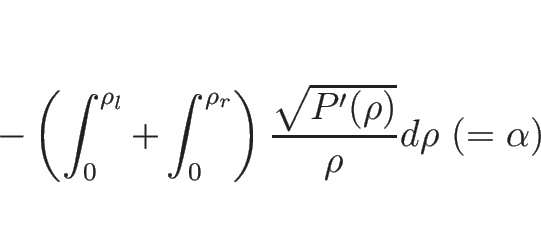
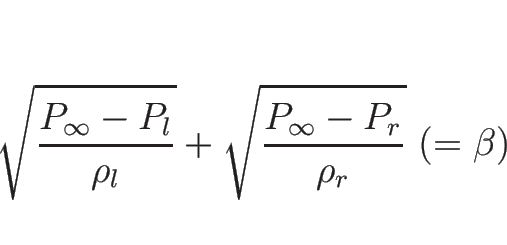
![]() のときは
のときは
![]() ,
,
![\begin{displaymath}
\int_0^{\rho_0}\frac{\sqrt{P'(\rho)}}{\rho}d \rho
= \left[\sqrt{A}\log\rho\right]_0^{\rho_0}
=\infty
\end{displaymath}](img1173.png)