また、![]() -特性方向が真性非線形である場合は、
-特性方向が真性非線形である場合は、
![]() -膨張波か
-膨張波か ![]() -衝撃波が起こり、
その左右の定数ベクトル
-衝撃波が起こり、
その左右の定数ベクトル ![]() と
と ![]() に対しては、
に対しては、
![]() が膨張波曲線
が膨張波曲線 ![]() 上にあるか、
上にあるか、
![]() が衝撃波曲線
が衝撃波曲線 ![]() 上にあるか、
のみが許される。なお、この
上にあるか、
のみが許される。なお、この ![]() と
と ![]() は、
相空間
は、
相空間 ![]() 上でいずれも
上でいずれも ![]() から出発する半曲線であるが、
実は、それらは綺麗につながることがわかる。
から出発する半曲線であるが、
実は、それらは綺麗につながることがわかる。
![]() -特性方向が真性非線形である場合、
-特性方向が真性非線形である場合、
![]() と
と ![]() は
は ![]() で
で ![]() で
(すなわち 2 階導関数まで連続に) つながる。
で
(すなわち 2 階導関数まで連続に) つながる。
証明
補題 4.2 より、![]() は、
は、
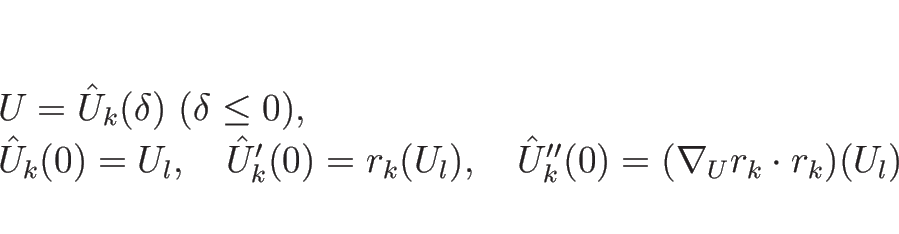
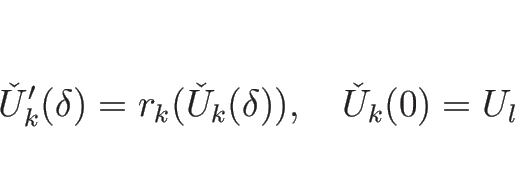
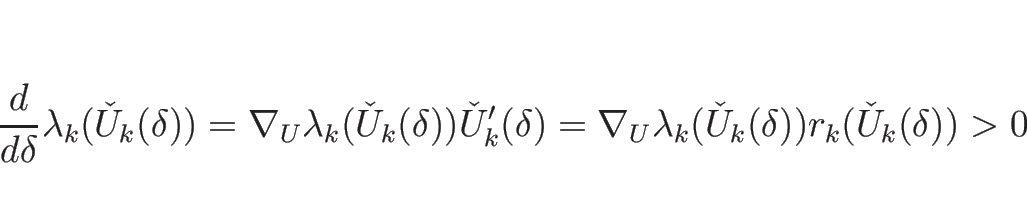
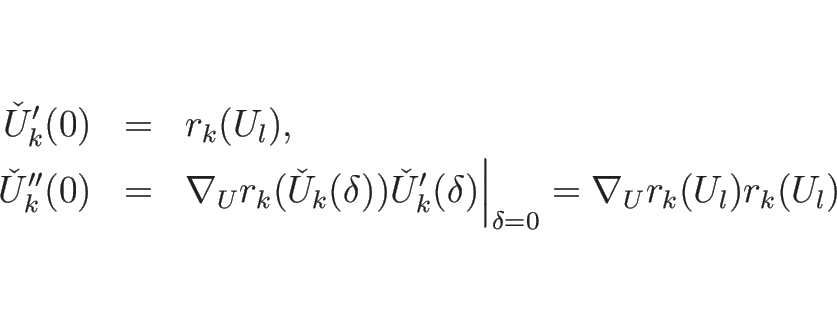
竹野茂治@新潟工科大学