5.1 はじめに
3 節、4 節で見てきたように、
保存則方程式
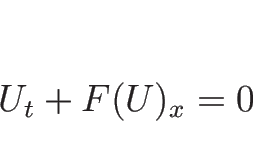 |
(5.109) |
は、膨張波、衝撃波、接触不連続といった単純な形の波の解を持つ。
この節では、この方程式 (5.1) の
いわゆるリーマン問題、すなわち初期値が
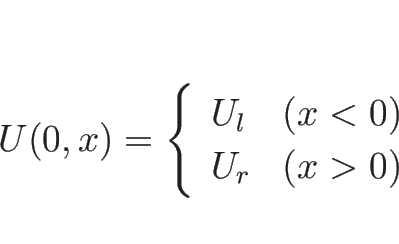 |
(5.110) |
であるような解を考えることにする。
ところで、よく、
なぜこのような初期値に対する問題を考えるのか、
と聞かれることがある。
それに対する理由のようなものを以下に紹介する。
- 保存則方程式は、初期値が滑らかな関数であっても、
衝撃波のような不連続な解が起こるが、
特に、衝撃波同士が衝突した後はどのようになるか、
ということを調べようと考えると、
それは局所的にはリーマン問題となる。
実際リーマンは、衝撃波同士の衝突後の様子の問題の一般化として
リーマン問題を考え始めたようである。
- 保存則方程式は、スケール変換
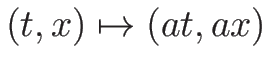 に対して
不変であるので、
に対して
不変であるので、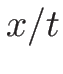 の関数の形の自己相似解を持つことになる。
そのような自己相似解の初期値問題は自然にリーマン問題となる。
の関数の形の自己相似解を持つことになる。
そのような自己相似解の初期値問題は自然にリーマン問題となる。
- いわゆる衝撃波管の実験に対応し、
工学的な応用面でも重要である。
なお、衝撃波管とは、長い管の真ん中に仕切りを置いて、
その両側を別な圧力や密度の気体で満たし、
ある瞬間にその仕切りを外し、その後の (高速に進む) 気体の変化を調べる、
という実験装置である。
- 現在知られている、保存則方程式の一般的な初期値に対する
解の存在証明のうち、Glimm の差分法や Lax-Friedrichs 差分、
Godunov 差分といった方法は、
このリーマン問題の解に基づいていて、
その解をブロックのように積み上げた近似解を評価し
極限を取ることで一般的な解を得る
(近似解を作る「煉瓦ブロック」と呼ばれることもある)。
しかもこれらの差分法は、
実際に計算機による数値計算に利用されることもあるので、
リーマン問題を解くことはそのような応用面でも重要である。
以下に、このリーマン問題の解を構成する、
これまで考察した単純波 (膨張波、衝撃波、接触不連続) の性質を
以下にまとめてみる。
なお、それらの波の中心は原点 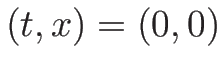 であるとし、
波の左右が定数ベクトル
であるとし、
波の左右が定数ベクトル 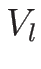 ,
, 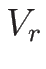 であるとする。
であるとする。
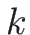 -特性方向:
-特性方向:
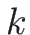 -膨張波,
-膨張波, 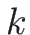 -衝撃波:
-衝撃波: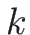 -特性方向が真性非線形のとき
-特性方向が真性非線形のとき
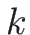 -接触不連続:
-接触不連続: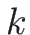 -特性方向が線形退化のとき
-特性方向が線形退化のとき
- 連続性:
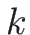 -膨張波:
-膨張波:- 連続 (つなぎ目はリプシッツ連続)
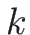 -衝撃波,
-衝撃波, 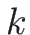 -接触不連続:
-接触不連続:- 不連続
- 波の範囲:
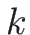 -膨張波:
-膨張波:-
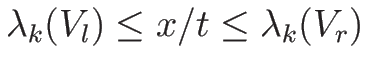 の扇形領域
の扇形領域
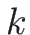 -衝撃波,
-衝撃波, 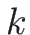 -接触不連続:
-接触不連続: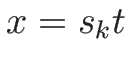 の一本の不連続線 (断層)
の一本の不連続線 (断層)
- 波と左右の特性速度との関係:
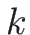 -膨張波:
-膨張波:- 波の両端は
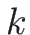 -特性速度に一致
-特性速度に一致
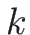 -衝撃波:
-衝撃波:-
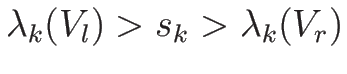
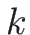 -接触不連続:
-接触不連続:-
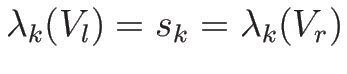
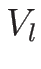 と
と 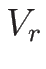 の関係:
の関係:
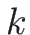 -膨張波:
-膨張波: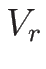 は
は 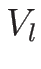 から出る
から出る 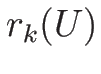 の積分曲線
(半曲線)
の積分曲線
(半曲線) 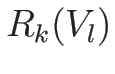 上
上
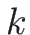 -衝撃波:
-衝撃波: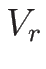 は
は 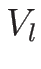 から出る半曲線
から出る半曲線 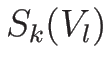 上
上
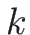 -接触不連続:
-接触不連続: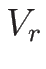 は
は 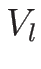 を通る
を通る
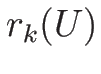 の積分曲線
の積分曲線 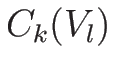 上 (
上 (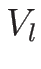 の両側)
の両側)
竹野茂治@新潟工科大学
2018-08-01
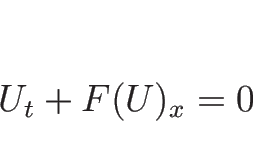
![]() であるとし、
波の左右が定数ベクトル
であるとし、
波の左右が定数ベクトル ![]() ,
, ![]() であるとする。
であるとする。