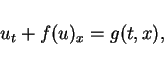 |
(1) |
In this paper we study a scalar conservation law with an outer force term
We consider the following problem:
Ifis a time-periodic function with period
, does a time-periodic solution exist with the same period, assuming the necessary condition
for the outer force termFor the existence of a time periodic solution, we need the decay of the solution to the homogeneous equation?
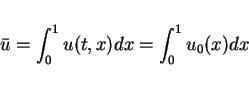
For the viscous equation
However, even in the scalar case, we cannot obtain
the time-periodic solution of our problem as the limit of
the periodic solutions of equation added ![]() to
(5) and (6) as
to
(5) and (6) as
![]() .
This is because the estimates for fast decay depend on the constant
.
This is because the estimates for fast decay depend on the constant
![]() and are not valid in the limit
and are not valid in the limit
![]() ,
and, according to [7], it does not imply that the decay
is fast for the limit equation (4).
,
and, according to [7], it does not imply that the decay
is fast for the limit equation (4).
On the other hand, the standard method for the proof of the existence of the weak solution to the equation (1) is to show the convergence of some approximate solutions which are constructed by a difference scheme method or the artificial viscosity method (5).
Tadmor ([13]) proved the slow decay for the Lax-Friedrichs difference approximations, which does not depend on the mesh size. Note that this is obtained from Oleinik's entropy condition ([11]) and from the periodicity of the boundary condition. We can to solve our problem by such a uniform estimate.
We remark that any such uniform estimates have not been obtained for the approximations of systems of conservation laws for large initial data, and therefore the existence of periodic solutions for systems of equations is still open.
Our result is the following.
We remark that the periodic solution of the problem (1),
(7) is not unique with respect to ![]() and
and ![]() .
.
The outline of the proof of Theorem 1 is the followings.
We construct a Lax-Friedrichs difference approximation for the problem
(1), (7)
and we will obtain the estimate of uniform bounds for it by the methods
similar to those of Tadmor ([13]) in §4.
The Poincare map is regarded as on the finite dimensional space for the
difference approximation because the approximate solution has values
at each finite point for fixed ![]() .
We show the map takes a closed convex set into the same set.
Hence we can use Brouwer's fixed point theorem for the existence of
the fixed point of the map from the continuity of the approximation.
Since these fixed points are uniformly bounded with respect to the
any mesh lengths, we obtain a subsequence that converges to
a weak solution by the compensated compactness theory ([15]).
We check the compactness of the entropy for the approximation in
§5 for the last convergence, and show the
limit is a weak solution of the problem (1),
(7) satisfying the entropy condition
in §6.
.
We show the map takes a closed convex set into the same set.
Hence we can use Brouwer's fixed point theorem for the existence of
the fixed point of the map from the continuity of the approximation.
Since these fixed points are uniformly bounded with respect to the
any mesh lengths, we obtain a subsequence that converges to
a weak solution by the compensated compactness theory ([15]).
We check the compactness of the entropy for the approximation in
§5 for the last convergence, and show the
limit is a weak solution of the problem (1),
(7) satisfying the entropy condition
in §6.