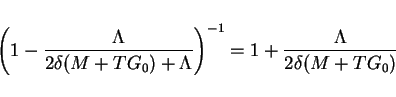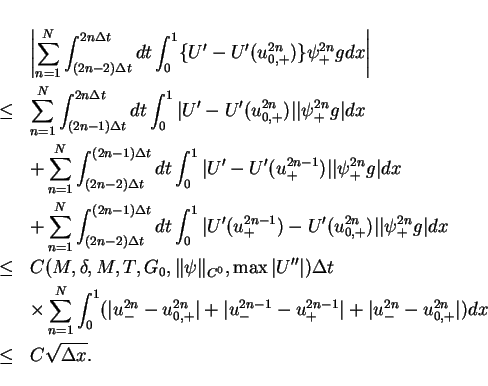

Next: Bibliography
Up: Time-periodic solutions
Previous: 5 Compactness of entropy
(PDF file: paper9.pdf)
6 Convergence to an entropy solution
In the last section, we saw the existence of a convergent sequence
of approximate. In this section, we show that the limit is a weak
solution and satisfies the entropy condition in this section.
To prove the limit is a weak solution,
it is sufficient that the integral
tends to zero as 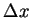 tends to zero for any
tends to zero for any
![$\phi\in C^1_0([0,T]\times[0,1])$](img216.gif) such that
such that
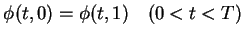 , because the data
, because the data
 is uniformly
bounded and have a subsequence which converges to a function
is uniformly
bounded and have a subsequence which converges to a function
 of
of  .
.
By the similar calculation in §5, it follows
since
![$\sigma[u^\Delta ]-[f^\Delta ]=0$](img218.gif) for shocks from the Rankine-Hugoniot
relation and
for shocks from the Rankine-Hugoniot
relation and
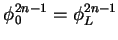 ,
where
,
where
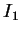 tends to zero because
tends to zero because
For 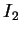 , we obtain
, we obtain
where
The function
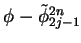 tends to zero because
tends to zero because
Therefore we obtain
Lastly, we show that the limit satisfies the entropy condition
(13). Let 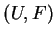 be a smooth entropy
pair and
be a smooth entropy
pair and 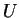 be a convex. The weak form of the entropy condition
is the inequality
be a convex. The weak form of the entropy condition
is the inequality
for any
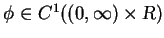 . It is sufficient
for the proof to show that
. It is sufficient
for the proof to show that
for
![$\psi\in C^1([0,T]\times[0,1])$](img232.gif) such that
such that
For convex entropy 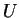 we can see
we can see
(cf. [3]). Hence,
since
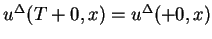 , where
, where
By 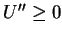 and
and
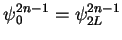 ,
,
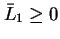 .
It follows by the similar way in §5 that
.
It follows by the similar way in §5 that
Hence we have
![\begin{displaymath}
\bar{I} \geq \int\hspace{-6pt}\int _{[0,T]\times[0,1]}U'g\psi dtdx + \bar{L}_2
+O(\sqrt{\Delta x}).\end{displaymath}](img242.gif) |
(29) |
From Taylor's expansion theorem
First two terms of the right hand side of (29) become
where 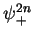 is a step value function defined by
is a step value function defined by
Remember the following lemma proved in [8].
LEMMA 6
Let
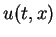
be the solution of the Riemann problem
(
16),
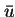
be the average of
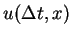
and the maximum wave speed
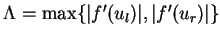
satisfy
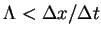
. Then
where
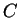
is a positive constant
For the approximation
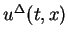 the constant
the constant 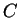 is
is
from (19). By Lemma 6
we estimate the rest term
Therefore, we obtain
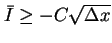 .
.


Next: Bibliography
Up: Time-periodic solutions
Previous: 5 Compactness of entropy
Shigeharu TAKENO
15 January 2002
![\begin{eqnarray*}
I & = & \int\hspace{-6pt}\int _{[0,T]\times[0,1]}(u^\Delta \p...
...+0,x)\phi(0,x)dx \\
& & - \int_0^1 u^\Delta (T+0,x)\phi(T,x)dx
\end{eqnarray*}](img215.gif)
![\begin{eqnarray*}
I & = & \int\hspace{-6pt}\int _{[0,T]\times[0,1]}(u^\Delta \p...
...+0,x)\phi(0,x)dx \\
& & - \int_0^1 u^\Delta (T+0,x)\phi(T,x)dx
\end{eqnarray*}](img215.gif)
![\begin{eqnarray*}
I & = & \int\hspace{-6pt}\int _{[0,T]\times[0,1]} g\phi dtdx
...
...int_0^1 \phi(u^{2n}_{0,+}-u^{2n}_{+})dx \\
& = & I_1 + I_2 \\
\end{eqnarray*}](img217.gif)
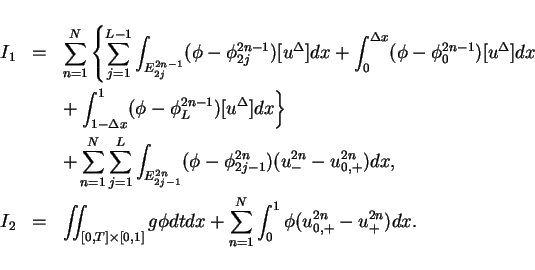
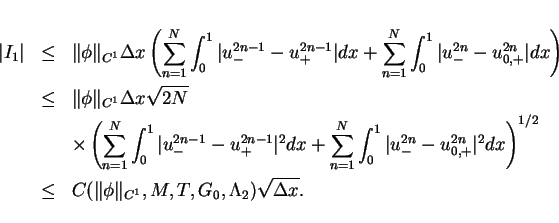
![\begin{eqnarray*}
I_2 & = & \int\hspace{-6pt}\int _{[0,T]\times[0,1]} g\phi dtd...
...{E_{2j-1}^{2n}} g(t,x)\{\phi(t,x)-\tilde{\phi}^{2n}_{2j-1}\} dx,
\end{eqnarray*}](img224.gif)
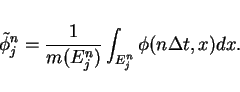
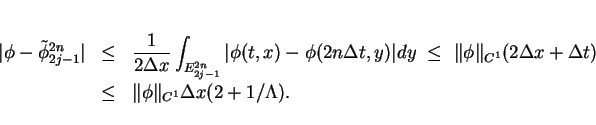
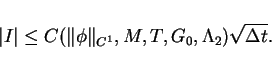
![]() be a smooth entropy
pair and
be a smooth entropy
pair and ![]() be a convex. The weak form of the entropy condition
is the inequality
be a convex. The weak form of the entropy condition
is the inequality
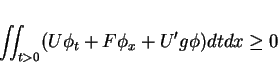
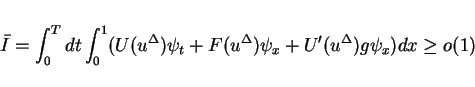
![\begin{displaymath}
\psi \geq 0,\hspace{1em}\psi(0,x)=\psi(T,x) \hspace{1em}(x\i...
...1]),\hspace{1em}
\psi(t,0)=\psi(t,1) \hspace{1em}(t\in [0,T]).
\end{displaymath}](img233.gif)
![\begin{displaymath}
\sigma[U]-[F] \geq 0
\end{displaymath}](img234.gif)
![\begin{eqnarray*}
\bar{I} & = & \sum_{n=1}^N \int_0^1 [U\psi]_{(2n-1)\Delta t+0...
...}_1 + \bar{L}_2 + \bar{L}_3
+\int\hspace{-6pt}\int U'g\psi dtdx
\end{eqnarray*}](img235.gif)
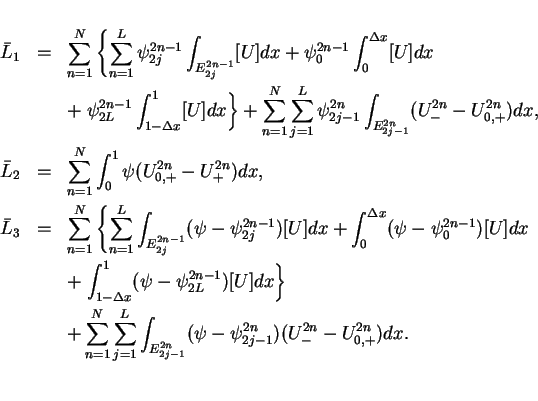
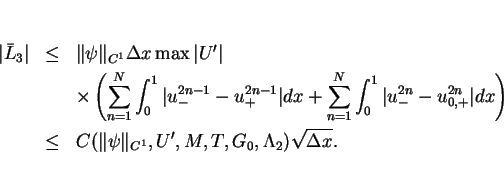
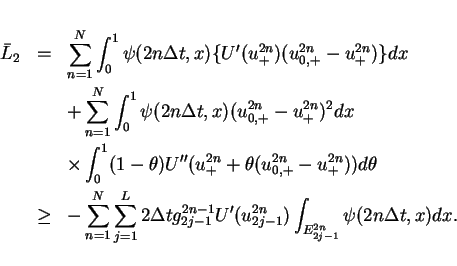
![\begin{eqnarray*}
& & \int\hspace{-6pt}\int _{[0,T]\times[0,1]}U'g\psi dtdx + \...
...\int_0^1\{U'-U'(u^{2n}_{0,+})\}
\psi^{2n}_{+}gdx + O(\Delta x),
\end{eqnarray*}](img244.gif)
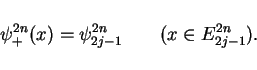
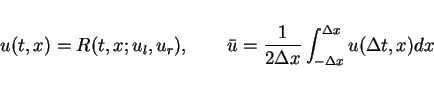
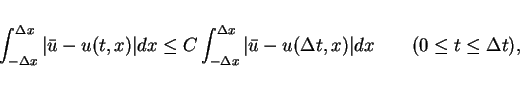
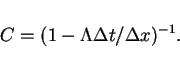
![]() the constant
the constant ![]() is
is