2.1 方針
3 次元の極座標は、
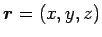 を
を
のように 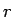 ,
, 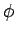 ,
, 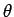 で表現する方法である。
地球表面の座標で言えば、
で表現する方法である。
地球表面の座標で言えば、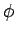 は経度、
は経度、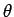 は緯度に対応する (例えば [1] 6.3 節参照。
ただし本稿は、この本の
は緯度に対応する (例えば [1] 6.3 節参照。
ただし本稿は、この本の 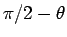 を
を 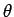 としている)。
としている)。
この 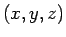 と
と
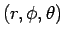 の関係を変数変換と考え、
の関係を変数変換と考え、
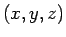 の関数
の関数 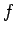 を
を
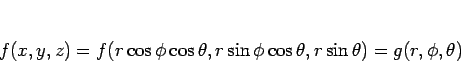
によって
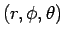 の関数
の関数 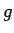 と見たときに、
「
と見たときに、
「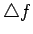 を
を 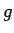 の微分で表現するとどうなるか」
というのが元の問題である。
の微分で表現するとどうなるか」
というのが元の問題である。
この場合、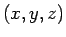 が
が
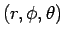 の式で表されているので、
の式で表されているので、
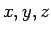 を
を 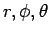 で微分するのはやさしいが、
その逆は難しい。
よって、この問題は通常以下のような方針によって求められる。
で微分するのはやさしいが、
その逆は難しい。
よって、この問題は通常以下のような方針によって求められる。
- 極座標の微分
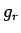 ,
, 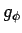 ,
, 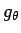 を 合成関数の微分を用いて
を 合成関数の微分を用いて 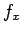 ,
, 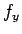 ,
, 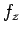 で表す (2.2 節)。
で表す (2.2 節)。
- そこから逆に
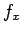 ,
, 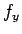 ,
, 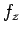 を
を 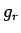 ,
, 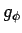 ,
, 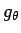 で表す (2.3 節)。
で表す (2.3 節)。
- それを用いて
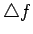 を
を 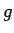 の微分で表現する (2.4, 2.5 節)。
の微分で表現する (2.4, 2.5 節)。
竹野茂治@新潟工科大学
2009年2月2日
![]() を
を
![]() と
と
![]() の関係を変数変換と考え、
の関係を変数変換と考え、
![]() の関数
の関数 ![]() を
を
![]() が
が
![]() の式で表されているので、
の式で表されているので、
![]() を
を ![]() で微分するのはやさしいが、
その逆は難しい。
よって、この問題は通常以下のような方針によって求められる。
で微分するのはやさしいが、
その逆は難しい。
よって、この問題は通常以下のような方針によって求められる。