2.3 極座標の微分での表現
次は (2), (3), (4) を 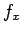 ,
, 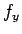 ,
, 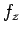 の連立方程式とみて解くことで、
の連立方程式とみて解くことで、
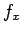 ,
, 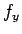 ,
, 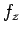 を極座標の微分
を極座標の微分 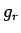 ,
, 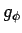 ,
, 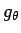 で表現する。
で表現する。
まず、(3) より
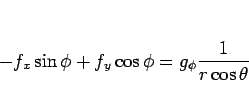 |
(5) |
(4) より
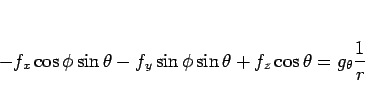 |
(6) |
となるので、
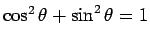 を用いれば (2)
を用いれば (2)
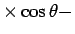 (6)
(6)
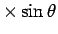 により、
により、
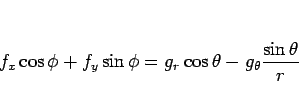 |
(7) |
となる。よって、
(7)
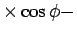 (5)
(5)
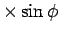 により
により
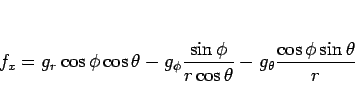 |
(8) |
と 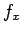 が得られ、
(7)
が得られ、
(7)
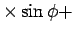 (5)
(5)
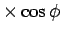 により
により
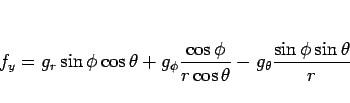 |
(9) |
と 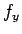 が得られる。
が得られる。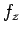 は、
(2)
は、
(2)
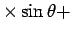 (6)
(6)
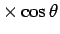 により
により
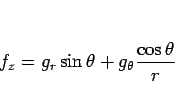 |
(10) |
となる。これで 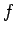 の微分が
の微分が 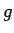 の微分で表されたことになる。
の微分で表されたことになる。
竹野茂治@新潟工科大学
2009年2月2日
![]() ,
, ![]() ,
, ![]() の連立方程式とみて解くことで、
の連立方程式とみて解くことで、
![]() ,
, ![]() ,
, ![]() を極座標の微分
を極座標の微分 ![]() ,
, ![]() ,
, ![]() で表現する。
で表現する。