2.4 2 階微分の計算
次はラプラシアン
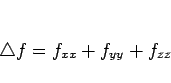
の計算のために、
(8), (9), (10) を繰り返し用いることで 2 階微分を計算する。
例えば 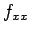 は、
は、
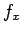 を
を 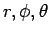 の関数と見たものを
の関数と見たものを 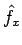 と書けば、
(8) より
と書けば、
(8) より
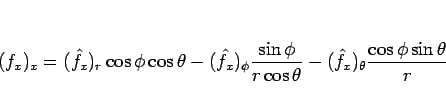
と書けることになるが、
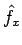 自体が (8) の右辺そのものなので、
自体が (8) の右辺そのものなので、
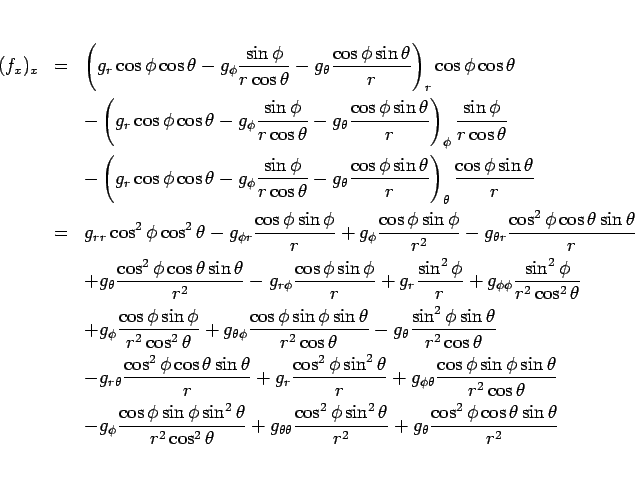
となり、これを整理して、
が得られる。
同様に (9) より、
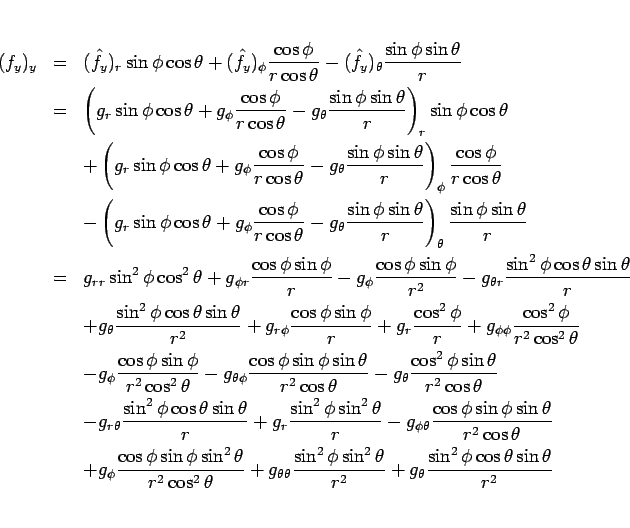
となるので、これを整理して、
となる。
そして最後に (10) より、
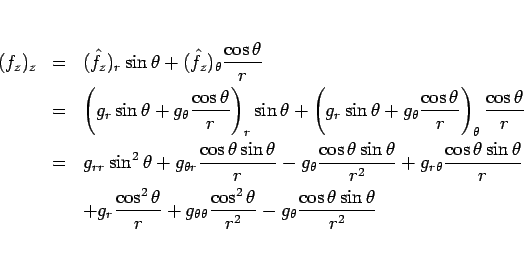
であるから、
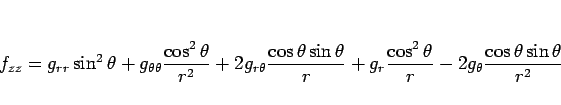 |
(13) |
となる。
竹野茂治@新潟工科大学
2009年2月2日
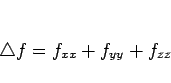
![]() は、
は、
![]() を
を ![]() の関数と見たものを
の関数と見たものを ![]() と書けば、
(8) より
と書けば、
(8) より