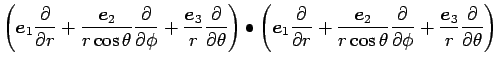 |
(20) |
(19) により、
任意のベクトル値関数
![]() ,
,
![]() 、
および任意の
、
および任意の ![]() ,
, ![]() に対して次が成り立つ。
に対して次が成り立つ。
証明
左辺に ![]() をつけると
をつけると
この命題 3 は、
![]() が形式的にスカラーであるとみて、
内積の左側のベクトルから右側のベクトルに移動できることを意味しているので、
それなりに自然なものに見える (もちろん前後の入れ換えは不可)。
が形式的にスカラーであるとみて、
内積の左側のベクトルから右側のベクトルに移動できることを意味しているので、
それなりに自然なものに見える (もちろん前後の入れ換えは不可)。
さて、まずは (20) の、
左のベクトルの ![]() での微分の項を考えると、
での微分の項を考えると、
![]() ,
,
![]() ,
,
![]() の成分には
の成分には ![]() は含まれないので、
命題 3 より
は含まれないので、
命題 3 より
(21)
次に、![]() での微分の項を考えるとこれは
での微分の項を考えるとこれは
(22)
最後に ![]() での微分の項であるが、
での微分の項であるが、
(23)
(24)
こちらの方もそれなりに手間はかかるのであるが、 2 節のやみくもな計算に比べると 内積で多くの項を消せる分楽であり、 見通しも立てやすいだろうと思う。
竹野茂治@新潟工科大学