6 アーベルの問題
(2017 年 3 月 22 日追加)
ここまで考察してきた「等時降下曲線」の問題を発展させた
「アーベルの問題」というものがあることを知ったので ([2] 13.4 節)、それもついでに紹介する。
これは、2 節の設定に対し、
「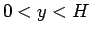 で正の値を取る関数
で正の値を取る関数 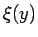 を与えたときに、
OA の経路の中の、高さ y の地点から O までに滑り落ちる時間が
を与えたときに、
OA の経路の中の、高さ y の地点から O までに滑り落ちる時間が
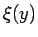 に等しくなるような曲線
に等しくなるような曲線 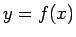 を求めよ」
を求めよ」
という問題のことであるらしい。
等時降下曲線は、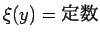 の場合であるから
アーベルの問題に含まれることになる。
の場合であるから
アーベルの問題に含まれることになる。
この問題は、(4) より、
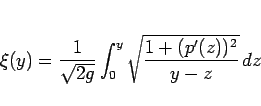 |
(12) |
となるような 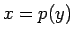 (
(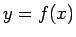 の逆関数) を求めることになる。
そして、(6) から (8) までと同等の
計算により、
の逆関数) を求めることになる。
そして、(6) から (8) までと同等の
計算により、
から、
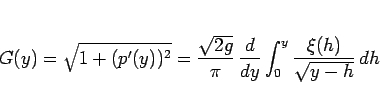 |
(13) |
となるので、この 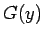 が求まれば
が求まれば
より
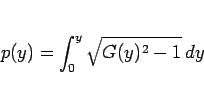 |
(14) |
と 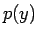 が求まることになる。なお、(13) より
が求まることになる。なお、(13) より
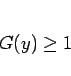 |
(15) |
である必要があるので、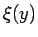 はなんでもよいわけではない。
はなんでもよいわけではない。
いくつか具体例を紹介する。
まず、等時の問題 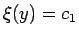 の場合には、
の場合には、
なので、
となり、(9) と同じ形になって確かにサイクロイドになる。
また、
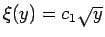 の場合は、
の場合は、
となるので、
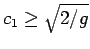 のときに
のときに
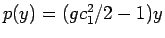 となる。
となる。
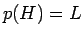 を課すことにすれば、
を課すことにすれば、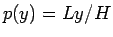 となり、
となり、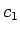 も
も
のように 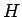 ,
, 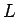 によって一意に決定する。
すなわち
によって一意に決定する。
すなわち 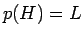 を課すと、
を課すと、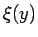 の定数
の定数 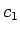 も
それによって決まってしまい、アーベルの問題が解けるための
も
それによって決まってしまい、アーベルの問題が解けるための 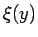 の自由度は高くないことがわかる。
の自由度は高くないことがわかる。
一方、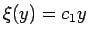 の場合は、
の場合は、
より
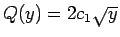 となるので、
となるので、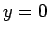 の近くでは条件 (15) を満たすことができない。
よって、この場合は
の近くでは条件 (15) を満たすことができない。
よって、この場合は 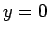 の近くまで含めた解は存在しないことになる。
の近くまで含めた解は存在しないことになる。
一般に 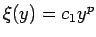 (
(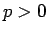 ) の場合は、
) の場合は、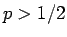 だと
だと 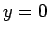 の近くでは条件 (15) を満たさず、
の近くでは条件 (15) を満たさず、
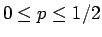 の場合に
の場合に
となり、よって
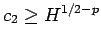 のときに
のときに
により 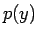 が求まることになる。
が求まることになる。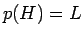 を課せば、
を課せば、
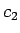 はやはり
はやはり 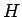 ,
, 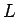 により一意に決まることになるだろう。
により一意に決まることになるだろう。
なお、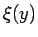 は必ずしも単調でなくてもよい。例えば、
は必ずしも単調でなくてもよい。例えば、
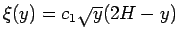 とするとこれは単調ではなく
とするとこれは単調ではなく 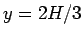 で極大を持つ関数で、そして、
で極大を持つ関数で、そして、
となるが、
なので、よって
となる。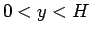 では
では
なので、この場合条件 (15) は
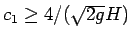 となり、この条件のもと
となり、この条件のもと
で求まることになる。この積分は、
を使えば計算できなくはないが、煩雑になるので省略する。
竹野茂治@新潟工科大学
2017年3月22日
で正の値を取る関数
を与えたときに、 OA の経路の中の、高さ y の地点から O までに滑り落ちる時間が
に等しくなるような曲線
を求めよ」
![]() の場合には、
の場合には、
![]() の場合は、
の場合は、
![]() の場合は、
の場合は、
![]() (
(![]() ) の場合は、
) の場合は、![]() だと
だと ![]() の近くでは条件 (15) を満たさず、
の近くでは条件 (15) を満たさず、
![]() の場合に
の場合に
![]() は必ずしも単調でなくてもよい。例えば、
は必ずしも単調でなくてもよい。例えば、
![]() とするとこれは単調ではなく
とするとこれは単調ではなく ![]() で極大を持つ関数で、そして、
で極大を持つ関数で、そして、