2 設定
まず問題を以下のように設定する。
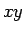 平面上の
平面上の
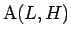 (
(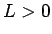 ,
, 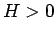 ) と 原点
) と 原点
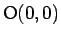 を
通る曲線
を
通る曲線 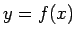 (
(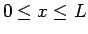 ) に沿って O に向かって玉を初速度 0 で
滑らす (またはころがす) とき、
AO 間のどの場所からスタートしても O に至る時間が変わらないような
関数
) に沿って O に向かって玉を初速度 0 で
滑らす (またはころがす) とき、
AO 間のどの場所からスタートしても O に至る時間が変わらないような
関数 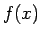 を求めよ (図 1)。
を求めよ (図 1)。
問題の設定より、明らかに
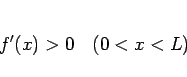 |
(1) |
である必要があることに注意する。よって、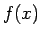 は増加関数となる。
は増加関数となる。
[1] で見たように、この曲線上の任意の点
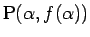 (
(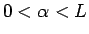 ) から初速 0 で
スタートした玉がすべって O に至るまでの時間
) から初速 0 で
スタートした玉がすべって O に至るまでの時間 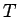 は、
は、
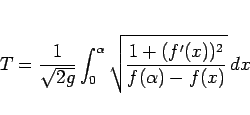 |
(2) |
で与えられる (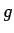 は重力加速度)。
ころがる場合も、半径が十分に小さいと考えれば
この定数倍となるだけだから、
結局 (2) が
は重力加速度)。
ころがる場合も、半径が十分に小さいと考えれば
この定数倍となるだけだから、
結局 (2) が 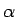 によらずに一定になるような
によらずに一定になるような 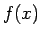 を
求めればいいことになる。
を
求めればいいことになる。
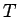 が
が 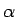 に関して一定であることから、
に関して一定であることから、
であり、通常はこの式から 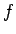 の微分方程式 (または積分方程式) を
導くのだが、(2) の被積分関数は
の微分方程式 (または積分方程式) を
導くのだが、(2) の被積分関数は 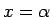 で特異性を持つので、
(2) は単純には微分できない。
よって別の方法を考える。
で特異性を持つので、
(2) は単純には微分できない。
よって別の方法を考える。
竹野茂治@新潟工科大学
2017年3月22日
平面上の
(
,
) と 原点
を 通る曲線
(
) に沿って O に向かって玉を初速度 0 で 滑らす (またはころがす) とき、 AO 間のどの場所からスタートしても O に至る時間が変わらないような 関数
を求めよ (図 1)。
![]() (
(![]() ) から初速 0 で
スタートした玉がすべって O に至るまでの時間
) から初速 0 で
スタートした玉がすべって O に至るまでの時間 ![]() は、
は、
![]() が
が ![]() に関して一定であることから、
に関して一定であることから、