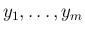
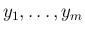 の独立性は、
の独立性は、
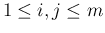 ,
, 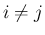 のすべての
のすべての 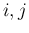 に対して
に対して
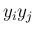 の係数
の係数 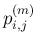 が 0 になることと同値になる。
よって、(56) より、それは
となる。なお、
が 0 になることと同値になる。
よって、(56) より、それは
となる。なお、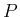 は対称行列で、よってこの行列の転置は
は対称行列で、よってこの行列の転置は 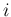 と
と 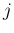 を
入れ替えたものになるので、これは
を
入れ替えたものになるので、これは 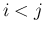 だけでなく、
だけでなく、
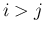 でも成り立つことに注意する。
でも成り立つことに注意する。
この条件 (57) を、元の行列 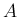 に対する条件に
書き直す。
に対する条件に
書き直す。
![$Q=[q_{i,j}]_{n,n}$](img376.png) とすると、
とすると、
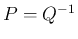 ,
, 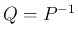 となる。
よって、系 4 により、
となる。ここで、
となる。
よって、系 4 により、
となる。ここで、
![$(1,\ldots,[k],\ldots,m)$](img379.png) は
は 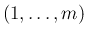 から
から 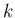 のみを取り除いた添字列、すなわち
のみを取り除いた添字列、すなわち
![$\displaystyle (1,\ldots,[k],\ldots,m) = (1,\ldots,k-1,k+1,\ldots,m)
$](img381.png)
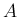 の行ベクトル
の行ベクトル
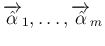 は線形独立なので、
は線形独立なので、
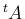 の列ベクトル
の列ベクトル
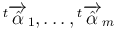 も
線形独立となり、補題 6 より
も
線形独立となり、補題 6 より 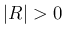 となる。
よって、
となる。
よって、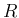 には逆行列
には逆行列 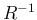 もあることになる。
もあることになる。
一方 (60) の最後の行列式は 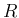 の余因子となるので、
条件 (57) は結局、
の余因子となるので、
条件 (57) は結局、
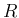 の余因子行列が対角行列以外 0 であることを意味し、
よって
の余因子行列が対角行列以外 0 であることを意味し、
よって 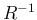 が対角行列であることと同値になる。
そしてそれは
が対角行列であることと同値になる。
そしてそれは 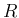 自身が対角行列であることと同値となるが、
自身が対角行列であることと同値となるが、
![$\displaystyle R=[\overrightarrow{\hat{\alpha}}_i\mathrel{・}\overrightarrow{\hat{\alpha}}_j]_{m,m}
$](img390.png)
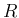 が対角行列であることは、
が対角行列であることは、
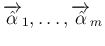 が
互いに垂直であることと同値になる。
が
互いに垂直であることと同値になる。
結局、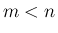 で
で 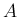 の行列が線形独立の場合も、
の行列が線形独立の場合も、
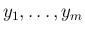 が独立であることは、
が独立であることは、
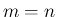 の場合と同じく、
の場合と同じく、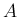 の行ベクトルが
互いに垂直であることと同値になる。
の行ベクトルが
互いに垂直であることと同値になる。
竹野茂治@新潟工科大学