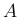
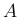 の行ベクトルが線形独立で、
かつ
の行ベクトルが線形独立で、
かつ 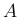 が正方行列でない場合、
すなわち
が正方行列でない場合、
すなわち 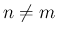 の場合となる。
の場合となる。
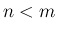 ならば
ならば  の行ベクトルは必ず線形従属となるので、
の行ベクトルは必ず線形従属となるので、
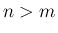 の場合のみを考えればよい。
の場合のみを考えればよい。
本節以降で、これをいくつかの段階に分けて、 補題などを紹介しながら考えていくことにする。
 次元行ベクトル
次元行ベクトル
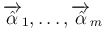 が線形独立なので、
これに
が線形独立なので、
これに 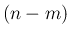 個の線形独立なベクトル
個の線形独立なベクトル
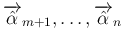 を追加して、
を追加して、
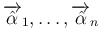 が線形独立であるようにできる。
が線形独立であるようにできる。
その上で
とすれば、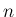 個の確率変数
個の確率変数
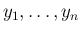 を作ることができる。
そして、
とし、
とする。
を作ることができる。
そして、
とし、
とする。
考えるのは、
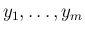 の独立性、
すなわち (10) であるが、
その左辺が
の独立性、
すなわち (10) であるが、
その左辺が 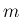 次元確率分布
次元確率分布
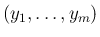 の分布関数
の分布関数
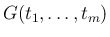 で、それを積分で書いて
で、それを積分で書いて
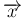 から
から
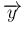 に
変数変換すれば、
に
変数変換すれば、
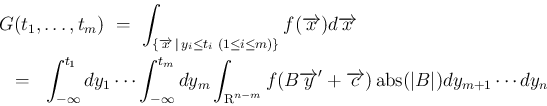
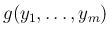 はこれを微分して、
となる。
あとは、これが
はこれを微分して、
となる。
あとは、これが
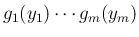 の形になるかどうかを
考えればよい。
ここで、
の形になるかどうかを
考えればよい。
ここで、
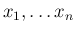 の独立性より、
の独立性より、
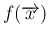 は (9) の形なので、
ここに
は (9) の形なので、
ここに
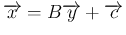 を代入すると、指数部分は、
(16) 同様
を代入すると、指数部分は、
(16) 同様
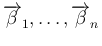 は線形独立なので、
は線形独立なので、
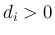 (
(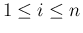 ) で、
よってこれを (9) に代入して、
(28) の積分を計算すると、最終的に、
) で、
よってこれを (9) に代入して、
(28) の積分を計算すると、最終的に、
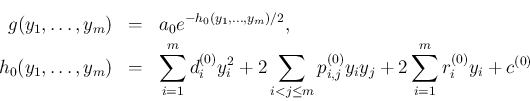
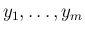 の独立性の条件は、
の独立性の条件は、
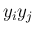 の係数
の係数 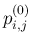 がすべて 0 になること、
になる。
がすべて 0 になること、
になる。
以後は、この 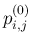 を具体的に求めること、
およびそれが 0 であるという条件を元の
を具体的に求めること、
およびそれが 0 であるという条件を元の 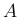 の条件に書き直すこと、
が目標となる。
の条件に書き直すこと、
が目標となる。
竹野茂治@新潟工科大学