A. 曲率の回転不変性
この節では補遺として、(10) または (19) によって
与えられる 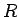 の回転不変性を示す。
もちろん 3 節や 4 節の議論から
それが回転不変性を持つことは明らかなのであるが、
それを式の上で (10), (19) に対して
直接示してみる。
の回転不変性を示す。
もちろん 3 節や 4 節の議論から
それが回転不変性を持つことは明らかなのであるが、
それを式の上で (10), (19) に対して
直接示してみる。
まず、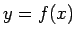 で表される曲線を回転して得られる曲線を考える。
点
で表される曲線を回転して得られる曲線を考える。
点 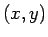 を原点の周りに
を原点の周りに 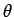 回転した点を
回転した点を
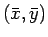 とすると、
それは
とすると、
それは
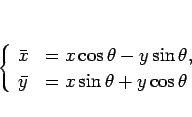 |
(21) |
となるので、これを 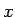 ,
, 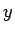 について解いて、
について解いて、
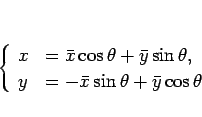 |
(22) |
とし、これを 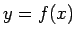 代入して得られる
代入して得られる 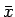 ,
, 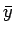 の式を
の式を 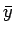 について解いて
について解いて
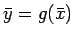 としたものが、
としたものが、
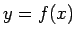 を
を 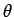 回転した曲線の式となる (
回転した曲線の式となる (
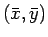 座標軸上のグラフ)。
座標軸上のグラフ)。
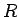 の回転不変性とは、
対応する点に対する
の回転不変性とは、
対応する点に対する 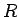 が
が 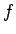 でも
でも 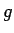 でも同じ値になること、すなわち、
でも同じ値になること、すなわち、
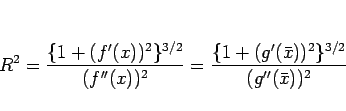 |
(23) |
が成り立つことであり、まずこれを示す (もちろん 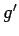 は
は 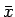 での微分を意味する)。
での微分を意味する)。
上で説明したように、(22) を 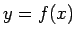 に代入した式
に代入した式
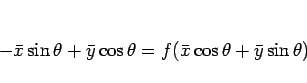
を 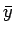 について解いたものが
について解いたものが
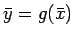 なので、
なので、
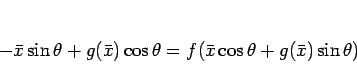 |
(24) |
となる。この式 (24) を 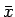 で微分すると、
で微分すると、
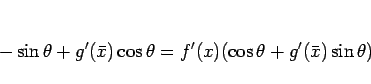 |
(25) |
となるから、これにより
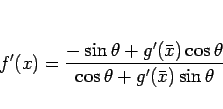 |
(26) |
が得られる。(25) を再び 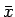 で微分すると、
で微分すると、
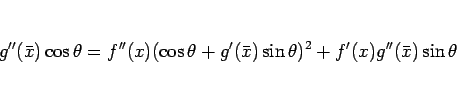
となるので、
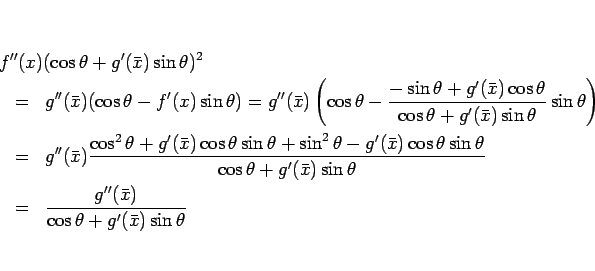
より、
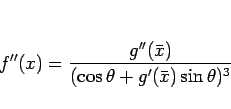 |
(27) |
となる。また、(26) より、
となるので、(27), (28) より
確かに (23) が成り立つことがわかる。
なお、2 節で 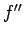 の値が回転不変ではないと書いたが、
それは (27) からわかる。
の値が回転不変ではないと書いたが、
それは (27) からわかる。
次に (19) の回転不変性であるが、これは
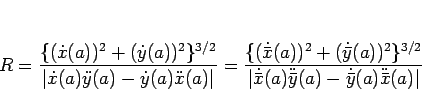 |
(29) |
ということである。
(22) より、
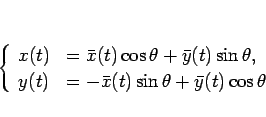
であるから、

となるから、(29) が成り立つことはすぐにわかる。
竹野茂治@新潟工科大学
2009年3月3日
![]() で表される曲線を回転して得られる曲線を考える。
点
で表される曲線を回転して得られる曲線を考える。
点 ![]() を原点の周りに
を原点の周りに ![]() 回転した点を
回転した点を
![]() とすると、
それは
とすると、
それは
![]() の回転不変性とは、
対応する点に対する
の回転不変性とは、
対応する点に対する ![]() が
が ![]() でも
でも ![]() でも同じ値になること、すなわち、
でも同じ値になること、すなわち、
![]() に代入した式
に代入した式
![]() の値が回転不変ではないと書いたが、
それは (27) からわかる。
の値が回転不変ではないと書いたが、
それは (27) からわかる。