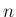 次正方行列
次正方行列 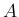 に対して、スカラー
に対して、スカラー 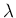 と、
と、
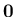 でない
でない 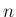 次元数ベクトル
次元数ベクトル
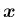 が、
が、
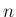 次正方行列
次正方行列 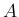 に対して、スカラー
に対して、スカラー 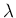 と、
と、
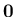 でない
でない 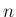 次元数ベクトル
次元数ベクトル
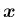 が、
が、
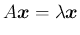
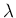 を
を 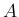 の固有値、
の固有値、
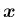 を
を 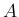 の、
の、
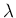 に関する固有ベクトルと言う。
に関する固有ベクトルと言う。
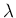 は
は
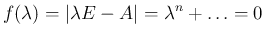
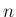 次方程式の解であり、一般には複素数となるが、
各
次方程式の解であり、一般には複素数となるが、
各 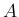 に対し重複も数えて、
に対し重複も数えて、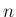 個存在する。
その各固有値
個存在する。
その各固有値 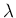 に対して、固有ベクトルは少なくとも一つは存在するが、
これも一般には複素数成分の数ベクトルとなる。
に対して、固有ベクトルは少なくとも一つは存在するが、
これも一般には複素数成分の数ベクトルとなる。
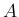 の成分がすべて実数で、
の成分がすべて実数で、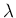 も実数であれば、
それに関する固有ベクトルは実数成分の数ベクトルが取れる。
も実数であれば、
それに関する固有ベクトルは実数成分の数ベクトルが取れる。
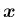 が
が 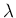 に関する固有ベクトルならば、
に関する固有ベクトルならば、
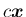 (
(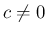 ) も
) も 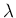 に関する固有ベクトル、
に関する固有ベクトル、
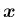 ,
,
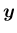 が
が 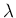 に関する固有ベクトルならば、
に関する固有ベクトルならば、
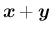 も
も 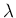 に関する固有ベクトルとなるので、
に関する固有ベクトルとなるので、
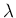 に関する固有ベクトル全体は、
に関する固有ベクトル全体は、
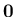 も入れれば、
1 次元以上の部分ベクトル空間を作る。
も入れれば、
1 次元以上の部分ベクトル空間を作る。
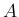 の
の 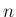 個の固有値
個の固有値
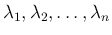 に対する
に対する
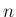 個の固有ベクトル
個の固有ベクトル
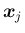 (
(
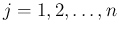 ) が存在するとき、
) が存在するとき、
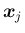 を並べた行列を
を並べた行列を
![$X=[\mbox{\boldmath$x$}_1\ \mbox{\boldmath$x$}_2\ \cdots\ \mbox{\boldmath$x$}_n]$](img95.png) とすると、
とすると、
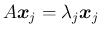 、および (3), (7) より、
、および (3), (7) より、
![\begin{eqnarray*}AX
&=&
A[\mbox{\boldmath$x$}_1\ \mbox{\boldmath$x$}_2\ \cdot...
...sh{\raisebox{.0ex}{\Large$O$}}& & & \lambda_n
\end{array}\right]\end{eqnarray*}](img97.png)
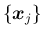 が一次独立であれば
が一次独立であれば 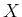 は逆行列を持つので、
と書ける。これを
は逆行列を持つので、
と書ける。これを 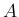 の対角化と呼ぶ。対角化により、例えば
の対角化と呼ぶ。対角化により、例えば 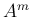 は
は
![\begin{eqnarray*}A^m
&=&
\left(X\left[\begin{array}{cccc}
\lambda_1 & & & \s...
...ebox{.0ex}{\Large$O$}}& & & \lambda_n^m
\end{array}\right]X^{-1}\end{eqnarray*}](img102.png)
さらに、行列 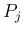 (
(
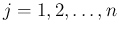 ) を
) を
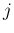 列目が
列目が
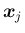 で、
それ以外の列はゼロベクトルとしたものである。すると、
で、
それ以外の列はゼロベクトルとしたものである。すると、
![$\displaystyle P_jX = [P\mbox{\boldmath$x$}_1\ P\mbox{\boldmath$x$}_2\ \cdots\ P...
...box{\boldmath$0$}\ \cdots\ \mbox{\boldmath$x$}_j\ \cdots\ \mbox{\boldmath$0$}]
$](img105.png)
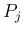 は、
は、
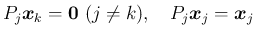
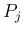 は、
は、
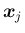 方向のベクトルは変えず、
方向のベクトルは変えず、
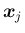 以外の方向のベクトルはすべて消すような行列で、
以外の方向のベクトルはすべて消すような行列で、
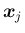 方向の射影行列と呼ばれる。
ここにさらに
方向の射影行列と呼ばれる。
ここにさらに 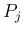 を左からかけると、
を左からかけると、
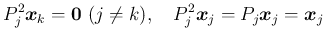
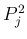 も (10) を満たすことになり、
よって
も (10) を満たすことになり、
よって 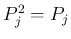 となる。また、
となる。また、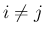 に対して、
に対して、
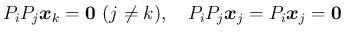
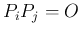 となることもわかる。すなわち射影行列は、
を満たす。
となることもわかる。すなわち射影行列は、
を満たす。
この射影行列により、 は
は
![$\displaystyle X
= [\mbox{\boldmath$x$}_1\ \mbox{\boldmath$x$}_2\ \cdots\ \mbox...
...ath$x$}_j\ \cdots\ \mbox{\boldmath$0$}]
= \sum_{j=1}^nP_jX
= (P_1+\cdots+P_n)X
$](img114.png)
![$\displaystyle AP_jX
= A[\mbox{\boldmath$0$}\ \cdots\ \mbox{\boldmath$x$}_j\ \c...
...\ \lambda_j\mbox{\boldmath$x$}_j\ \cdots\ \mbox{\boldmath$0$}]
= \lambda_jP_jX
$](img115.png)
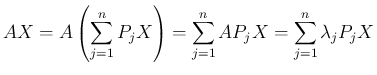
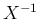 を右からかければ、
が得られる。これは、
を右からかければ、
が得られる。これは、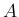 の対角化 (9) の射影行列による
表現であり、行列のスペクトル分解とも呼ばれる。
この場合も、例えば
の対角化 (9) の射影行列による
表現であり、行列のスペクトル分解とも呼ばれる。
この場合も、例えば 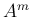 は、(11) の性質により、
は、(11) の性質により、
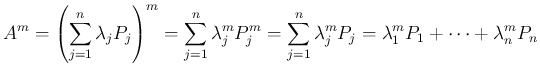
竹野茂治@新潟工科大学