![$A=[a_{ij}]_{m,n}$](img2.png)
![$A=[a_{ij}]_{m,n}$](img2.png) 、
、
![$B=[b_{ij}]_{n,p}$](img4.png) とし、
2 節同様に
とし、
2 節同様に 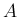 ,
, 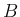 の
列ベクトルを
の
列ベクトルを
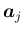 (
(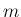 次元),
次元),
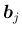 (
(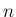 次元),
行ベクトルの転置を
次元),
行ベクトルの転置を
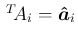 (
(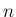 次元),
次元),
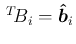 (
(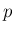 次元) と書くことにする。
次元) と書くことにする。
![$\displaystyle A = [\mbox{\boldmath$a$}_1\ \mbox{\boldmath$a$}_2\ \cdots\ \mbox{...
...}$}_2}}\\ \vdots\\ {\,{}^T\!{\mbox{\boldmath$\hat{b}$}_n}}
\end{array}\right]
$](img34.png)
![$\displaystyle \mbox{\boldmath$a$}_j = \left[\begin{array}{c}{a_{1j}}\\ {a_{2j}}...
...ft[\begin{array}{c}{b_{i1}}\\ {b_{i2}}\\ \vdots\\ {b_{ip}}
\end{array}\right]
$](img35.png)
さて、積 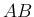 は、
は、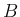 を列ベクトルで表すことで、
まず次の形に書くことができる。
を列ベクトルで表すことで、
まず次の形に書くことができる。
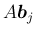 の形の行列の積で、
これは
の形の行列の積で、
これは 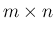 行列と
行列と 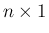 行列 (列ベクトル) の積だから
行列 (列ベクトル) の積だから
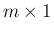 行列の
行列の 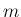 次元列ベクトルとなり、
よって結果としてそれが
次元列ベクトルとなり、
よって結果としてそれが 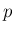 個並んだ
個並んだ 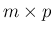 行列となる。
行列となる。
見た目はベクトルのスカラー倍のような計算にも見えるが、
実際には各列が行列の積になっているわけである。証明は、
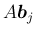 の上から
の上から 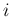 番目の成分が、
番目の成分が、
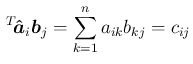
次に、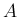 を行ベクトルで表すことで、次の形にも書くことができる。
を行ベクトルで表すことで、次の形にも書くことができる。
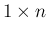 行列
行列
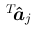 と
と 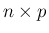 行列
行列 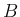 の積である
の積である 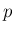 次元の行ベクトルで、
よって
次元の行ベクトルで、
よって 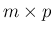 行列になっている。
行列になっている。
これも、証明は、
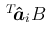 の左から
の左から 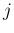 番目の成分が、
番目の成分が、
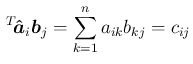
さらに、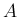 を行ベクトル、
を行ベクトル、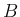 を列ベクトルで表すと、
を列ベクトルで表すと、
これも、一見 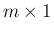 行列と
行列と 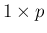 行列の積にも見え、
そしてそれと同じ計算をしているようだが、
各要素が
行列の積にも見え、
そしてそれと同じ計算をしているようだが、
各要素が
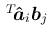 という
という 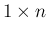 行列と
行列と 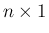 行列の積、
すなわち、
行列の積、
すなわち、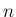 次元ベクトル同士の内積
次元ベクトル同士の内積
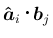 になっていて、単純なスカラー同士の積ではない。
になっていて、単純なスカラー同士の積ではない。
これも証明は、その 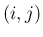 成分が
成分が
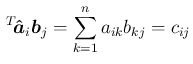
また、逆に 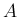 を列ベクトル、
を列ベクトル、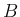 を行ベクトルで表すと、
を行ベクトルで表すと、
これは、一見 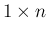 行列と
行列と 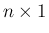 行列の積と同じ計算にも
見えるが、実際には、各項が
行列の積と同じ計算にも
見えるが、実際には、各項が 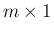 行列
行列
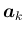 と
と 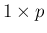 行列
行列
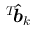 の積、
すなわち
の積、
すなわち 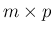 行列となっていて、
すなわち
行列となっていて、
すなわち 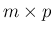 行列の
行列の 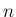 個の和になっている。
個の和になっている。
この証明は、
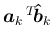 の
の 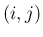 成分が
成分が 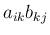 のただ 1 項であり、
よって (6) の右辺の
のただ 1 項であり、
よって (6) の右辺の 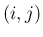 成分が
成分が
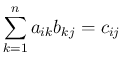
また、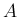 を列ベクトル、
を列ベクトル、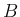 を成分で表せば、
を成分で表せば、
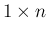 行列と
行列と 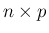 行列の
積の計算のようにも見える。
行列の
積の計算のようにも見える。
この証明は、
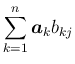 の上から
の上から 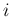 番目の成分が
番目の成分が
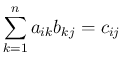
逆に、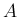 を成分、
を成分、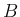 を行ベクトルで表せば、
を行ベクトルで表せば、
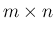 行列と
行列と 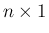 行列の
積の計算のようにも見える。
行列の
積の計算のようにも見える。
この証明は、
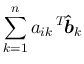 の
左から
の
左から 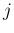 番目の成分が
番目の成分が
竹野茂治@新潟工科大学