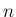 個の
個の 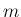 次元数ベクトル
次元数ベクトル
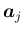 (
(
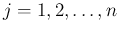 ,
, 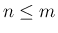 ) が、
単位ベクトルで、互いに垂直であるとき、それらの内積は
) が、
単位ベクトルで、互いに垂直であるとき、それらの内積は
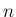 個の
個の 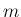 次元数ベクトル
次元数ベクトル
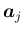 (
(
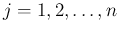 ,
, 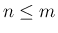 ) が、
単位ベクトルで、互いに垂直であるとき、それらの内積は
) が、
単位ベクトルで、互いに垂直であるとき、それらの内積は
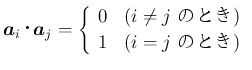
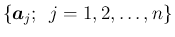 の組は、
の組は、
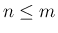 でなければ取ることはできない。
このとき、それを並べた行列
でなければ取ることはできない。
このとき、それを並べた行列
![$\displaystyle A = [\mbox{\boldmath$a$}_1\ \mbox{\boldmath$a$}_2\ \cdots\ \mbox{\boldmath$a$}_n]
$](img75.png)
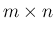 行列となるが、
行列となるが、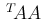 は (5) により、
は (5) により、
![$\displaystyle \,{}^T\!{A}A
=
\left[\begin{array}{c}{\,{}^T\!{\mbox{\boldmath$a...
..._j]_{n,n}
=
[\mbox{\boldmath$a$}_i\mathop{・}\mbox{\boldmath$a$}_j]_{n,n}
= E_n
$](img77.png)
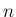 次の単位行列になる。
次の単位行列になる。
特に、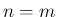 の場合は、
の場合は、
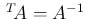 となり、
となり、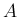 は直交行列となる。
すなわち、
は直交行列となる。
すなわち、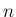 個の互いに垂直な
個の互いに垂直な 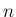 次元の単位ベクトルを列ベクトルとする
次元の単位ベクトルを列ベクトルとする
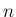 次の正方行列は直交行列となるし、逆に直交行列の列ベクトルは、
互いに垂直な単位ベクトルとなる。
次の正方行列は直交行列となるし、逆に直交行列の列ベクトルは、
互いに垂直な単位ベクトルとなる。
竹野茂治@新潟工科大学