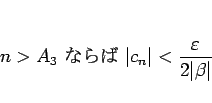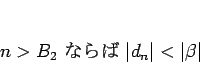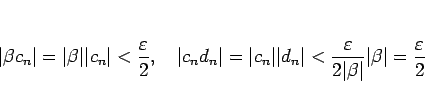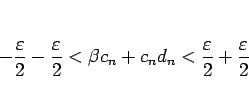次へ: 6 関数の収束
上へ: ε-δのお話
前へ: 4 への発散
(PDF ファイル: epsdlt1.pdf)
5 積の収束の証明
では、3 節の極限の定義 2 を使って、
積の収束 (3) を証明してみよう。
この場合、どんな 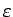 (
(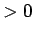 ) に対しても、
) に対しても、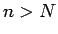 ならば
ならば
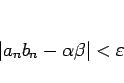 |
(6) |
となるような 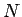 が取れればいい。そのような
が取れればいい。そのような 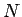 を実際に探してみる。
を実際に探してみる。
まず、2 節のように、
とすると、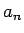 ,
, 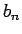 は
は 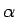 ,
, 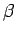 にそれぞれ収束する
という仮定から、
極限の定義 2 により、
どんな
にそれぞれ収束する
という仮定から、
極限の定義 2 により、
どんな 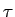 (
(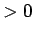 ) に対しても
) に対しても
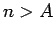 ならば
ならば
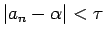 となるような
となるような 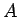 が取れ、
が取れ、
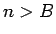 ならば
ならば
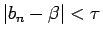 となるような
となるような 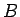 が取れる
が取れる
はずである。つまり、この場合、
となることになる。
2 節で計算したように、
であることに注意する。
まず、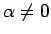 ,
, 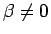 の場合を考える。
の場合を考える。
仮定より、
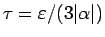 と考えれば、
と考えれば、
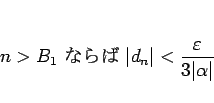 |
(7) |
となるような 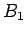 が取れるはずである。
同様に、
が取れるはずである。
同様に、
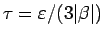 と考えれば
と考えれば
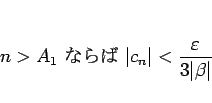 |
(8) |
となるような 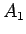 が取れるはずであるし、
が取れるはずであるし、
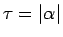 と考えれば
と考えれば
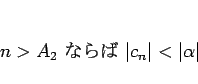 |
(9) |
となるような 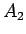 も取れるはずである。
も取れるはずである。
この、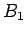 ,
, 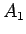 ,
, 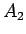 の一番大きいものを
の一番大きいものを 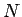 としよう。
そうすると、
としよう。
そうすると、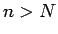 ならば、もちろん
ならば、もちろん 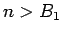 だから
(7) より
だから
(7) より
なので、
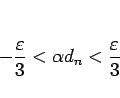 |
(10) |
となる。同様に 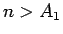 だから (8) より
だから (8) より
なので、
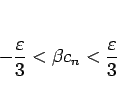 |
(11) |
である。そして、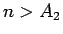 かつ
かつ 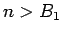 だから、
(7) と (9) より
だから、
(7) と (9) より
なので、
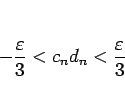 |
(12) |
である。この (10),(11),(12) を
合わせると、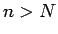 に対しては
に対しては
すなわち、
が言え、(6) が言えることになる。
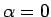 で
で 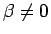 のときは、
のときは、
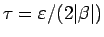 とすれば
とすれば
である 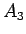 が取れ、
が取れ、
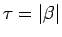 とすれば
とすれば
であるような 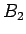 が取れる。
よって、
が取れる。
よって、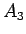 と
と 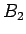 の大きい方を
の大きい方を 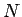 とすれば、
とすれば、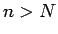 であれば
であれば
なので、
となり、よって
が言える。その他の場合も同様である。
次へ: 6 関数の収束
上へ: ε-δのお話
前へ: 4 への発散
竹野茂治@新潟工科大学
2006年3月31日
![]() (
(![]() ) に対しても、
) に対しても、![]() ならば
ならば
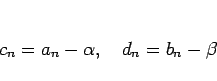
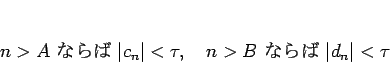
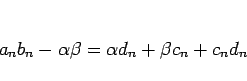
![]() と考えれば、
と考えれば、
![]() ,
, ![]() ,
, ![]() の一番大きいものを
の一番大きいものを ![]() としよう。
そうすると、
としよう。
そうすると、![]() ならば、もちろん
ならば、もちろん ![]() だから
(7) より
だから
(7) より
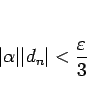
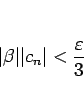
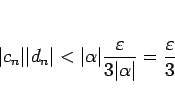
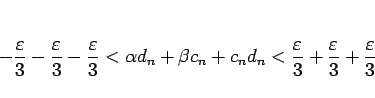
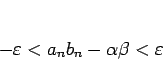
![]() で
で ![]() のときは、
のときは、
![]() とすれば
とすれば