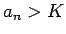次へ: 5 積の収束の証明
上へ: ε-δのお話
前へ: 3 0 への収束
(PDF ファイル: epsdlt1.pdf)
4 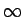 への発散
への発散
ついでに、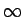 への発散
への発散
も定義してみる。この場合は、
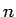 が大きくなるとき、
が大きくなるとき、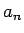 の値は限りなく大きくなる
の値は限りなく大きくなる
ということを意味していて、「限りなく大きくなる」とは
「大きくなる度合いに際限がない」「いくらでも大きくなる」
ということを意味する。例えば次のような数列は限りなく大きくなる。
しかし、次のような数列は「限りなく大きく」はならない。
上の方の例は、だんだん大きくはなっているが、1 より大きくなることはないし、
また、下の方の例は、全部そろって大きくなっているわけではなく、飛び飛びに
大きくないものが含まれている。これらは「いくらでも大きくなる」とはいいがたい。
よって、「限りなく大きくなる」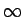 への発散は、次のように定義される。
への発散は、次のように定義される。
定義 3
とは、どんな正の数 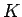 (
(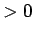 ) を取っても、
) を取っても、
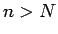 ならば
ならば 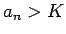
となるような 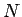 を取ることができること、を意味する。
を取ることができること、を意味する。
次へ: 5 積の収束の証明
上へ: ε-δのお話
前へ: 3 0 への収束
竹野茂治@新潟工科大学
2006年3月31日
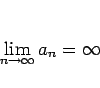
が大きくなるとき、
の値は限りなく大きくなる
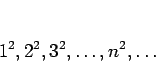
![]() への発散は、次のように定義される。
への発散は、次のように定義される。
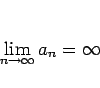
ならば