のように書かれている。 しかし、これは極限の意味を感覚的に伝えている「説明」にすぎず、 数学的に厳密な「定義」とは言いがたく、 例えば「限りない」とはどういうことか、といったような説明はそこにはない。が大きくなるときに、数列
の値が限りなく
に近づくこと
例えば、これを定義とみて、次の性質
証明すべきことはなので、 つまり、
を示せばよい。が大きくなるときに、数列
の値が限りなく
に近づくこと
は限りなく
に近づいていくので、
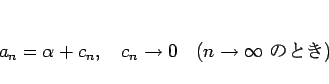
と書ける。同様に、
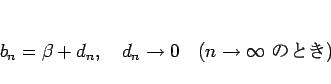
と書けるので、
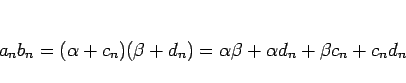
となるが、
なので、,
,
より
となり、確かにこの「証明らしきもの」は一見正しいように見えるかもしれないが、 最後の段階の (4) から (5) を導くところで この命題の結論自身、すなわちの値は限りなく
に近づく。
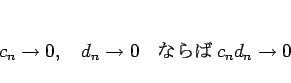
しかし逆に言えば、この場合、すなわち 0 に収束する場合
(![]() ,
, ![]() の場合) を示せば、
一般の場合 (
の場合) を示せば、
一般の場合 (![]() ,
, ![]() の場合) の場合は
それを使って証明できることになりそうだとわかる。
の場合) の場合は
それを使って証明できることになりそうだとわかる。
よって今度は、これも含めて「0 に収束する」 ということを考えてみることにする。