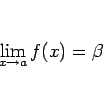
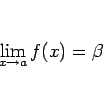
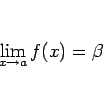
となるようなかつ
ならば
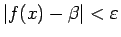
なお、ここに「![]() 」というものが入っているが、
関数の極限では
」というものが入っているが、
関数の極限では ![]() での値、
すなわち
での値、
すなわち ![]() が
が ![]() に近いかどうかは問わない
(逆に、この極限
に近いかどうかは問わない
(逆に、この極限 ![]() が
が ![]() に等しいときは
に等しいときは
![]() は
は ![]() で「連続」であるという)。
で「連続」であるという)。
このような極限の定義は A.L.Cauchy (1789-1857, 仏)
によって始められた極限の定義方法であるが、
よく「![]() -
- ![]() 論法」と呼ばれている。
論法」と呼ばれている。
理学部数学科向けの数学の本では、英語を直訳したような独特の表現で、
任意の正数のように書いたり、さらに「任意の」を「(
) に対して ある
(
) が存在し、
となるかつ
ならば
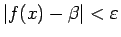
のように書いたりすることもある。 慣れればなんでもないのであるが、 初学者はこのような妙な言いまわしにとまどうことも多い。(
),
(
), s.t.
かつ
ならば
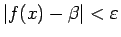
(s.t.such that (
を満たすような))