2.3 Riemann 問題の解
膨張波、衝撃波、接触不連続は、その波と特性速度との関係
(2.5),
(2.8),
(2.10)
から、次のことがわかる:
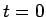 で
で 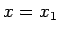 から出る
から出る 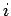 -波
(
-波
(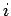 -膨張波、
-膨張波、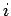 -衝撃波、
-衝撃波、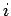 -接触不連続) と、
定ベクトル
-接触不連続) と、
定ベクトル 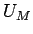 をはさんで右に
をはさんで右に 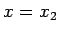 (
(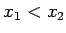 ) から出る
) から出る
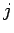 -波を並べたとき、
-波を並べたとき、
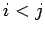 ならば
ならば 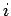 -波と
-波と 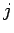 -波は遠ざかる
-波は遠ざかる
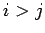 ならば
ならば 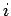 -波と
-波と 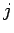 -波は近づいて、ある時刻でぶつかる
-波は近づいて、ある時刻でぶつかる
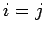 のときは、
のときは、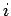 -波と
-波と 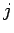 -波の少なくとも一方が衝撃波のときは
近づいてぶつかり、いずれも衝撃波でないとき
(両方が膨張波、または両方が接触不連続) は、
両者の波の間隔は一定のままで、近づきもしないし、離れもしない。
-波の少なくとも一方が衝撃波のときは
近づいてぶつかり、いずれも衝撃波でないとき
(両方が膨張波、または両方が接触不連続) は、
両者の波の間隔は一定のままで、近づきもしないし、離れもしない。
そして、これにより、
一般の Riemann 問題 (1.1), (1.2)
の解は、1-波、2-波、...、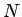 -波を左から右に順に並べて作れること、
すなわち、
-波を左から右に順に並べて作れること、
すなわち、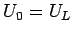 ,
, 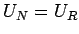 に対し
に対し
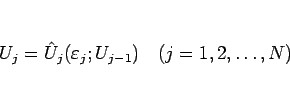
となる
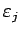 (
(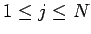 ) を求めることで、
) を求めることで、
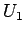 から
から 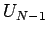 までの定ベクトル状態を扇型で挟むような
までの定ベクトル状態を扇型で挟むような
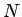 個の波により作られることがわかる
(図 2.1,2.2)。
個の波により作られることがわかる
(図 2.1,2.2)。
図 2.1:
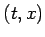 平面での解の表現
平面での解の表現
![\begin{figure}
\psfrag{x}{$x$}
\psfrag{t}{$t$}
\psfrag{0}{$0$}
\psfrag{...
...cludegraphics[width=0.2\textheight]{riemann_tx.eps}
\end{center} \end{figure}](img108.gif) |
図 2.2:
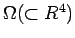 での各曲線
での各曲線
![\begin{figure}
\psfrag{U0=UL}{$U_0=U_L$}
\psfrag{U1}{$U_1=\hat{U}_1(\varepsil...
...ludegraphics[width=0.2\textheight]{riemann_omg.eps}
\end{center} \end{figure}](img109.gif) |
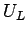 ,
, 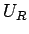 が十分近ければ、その Rimann 問題の解は、
このような形としては一意的に解が求まる。
竹野茂治@新潟工科大学
が十分近ければ、その Rimann 問題の解は、
このような形としては一意的に解が求まる。
竹野茂治@新潟工科大学
2009年1月18日
で
から出る
-波 (
-膨張波、
-衝撃波、
-接触不連続) と、 定ベクトル
をはさんで右に
(
) から出る
-波を並べたとき、