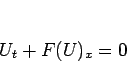 |
(1.1) |
(1.1)
Glimm の差分法 ([Glimm]) は、Riemann 問題と呼ばれる (1.1) の初期値問題
(1.2)
![]() 、すなわち単独の方程式の場合には、
いわゆる Lax-Friedrichs の差分法による近似解、および人工粘性近似解が
有界変動評価を持ち、よって Helly の選出定理によりその極限として
弱解が得られることが先に示されている ([Oleinik])。
Glimm の証明では、近似解の収束性の証明はそれと同じ手法を使っているので、
連立方程式の場合に同様の評価を示すことを目標とする点は単純なのであるが、
それ以外の部分である近似解の作り方、有界変動評価を示すための種々の補題、
誤差評価に対する考察等が、当時 (1965 年) のこの分野の状況からして
極めて独創的な手法であり、まさに無から有を生み出したごとき論文で1、
そして保存則方程式では基本的で非常に重要な結果でもある。
保存則方程式の数少ない日本語の解説記事である [西田-川島] には、
、すなわち単独の方程式の場合には、
いわゆる Lax-Friedrichs の差分法による近似解、および人工粘性近似解が
有界変動評価を持ち、よって Helly の選出定理によりその極限として
弱解が得られることが先に示されている ([Oleinik])。
Glimm の証明では、近似解の収束性の証明はそれと同じ手法を使っているので、
連立方程式の場合に同様の評価を示すことを目標とする点は単純なのであるが、
それ以外の部分である近似解の作り方、有界変動評価を示すための種々の補題、
誤差評価に対する考察等が、当時 (1965 年) のこの分野の状況からして
極めて独創的な手法であり、まさに無から有を生み出したごとき論文で1、
そして保存則方程式では基本的で非常に重要な結果でもある。
保存則方程式の数少ない日本語の解説記事である [西田-川島] には、
「グリムの差分法は、方程式系の弱解の構成およびその性質を知るための 現在あるほぼ唯一の手段であり、それと同時に方程式系を理解するための 一つの関門になっている。この方面を勉強しようと思う読者は是非とも [Glimm] に挑戦していただきたい。」と書かれている。 ただ、この [Glimm] は短い論文でそれなりに難しく、 初学者にはやはり大変なのではないかと思う。
しばらくの間、この保存則方程式の分野の教科書は [Smoller] (初版は 1983 年出版) しかなかったが、 近年次々と教科書風の本が出版されてきているし (例えば、[Serre], [Dafermos], [Bressan], [Zheng], [LeFloch], [Perthame], [Holden-Risebro], [Lu])、 Glimm の差分法も、元々の [Glimm] の証明は よりわかりやすく改良され、 説明されるようになってきている。
よって本稿では、連立の保存則方程式に対する Glimm の証明を、 それら改良された方法を導入しながら解説することを目標とする。 ほぼ [Dafermos] に書かれている内容に沿った形で紹介するが、 [Dafermos] には [Young] 等により追加された結果なども 含まれているので、本稿では必要最小限に説明していきたい。
竹野茂治@新潟工科大学