2.4 Riemann 問題の解の評価
後で必要となる、Riemann 問題の解の評価をここで行っておく。
今、
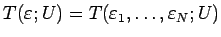 を、
を、
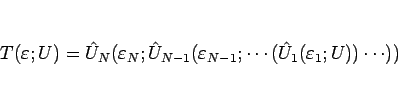
と書くこととすれば、Riemann 問題は、
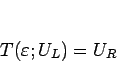 |
(2.14) |
を満たす
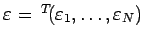 を求めることに帰着される。それは陰関数定理によるのであるが、
を求めることに帰着される。それは陰関数定理によるのであるが、
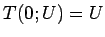 であり、また
であり、また
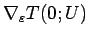 は、
は、
より、
![\begin{displaymath}
\left.\nabla_\varepsilon \{T(\varepsilon ;U_L)-U_R\}
\right\...
...psilon =0,U_L=U_R=\bar{U}}
=[r_1(\bar{U}),\ldots,r_N(\bar{U})]
\end{displaymath}](img120.gif)
となる。この右辺は正則行列だから、陰関数定理により
方程式 (2.12) を
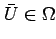 の近傍で
の近傍で
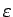 について解くことができる。
具体的には、ある正数
について解くことができる。
具体的には、ある正数
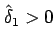 が存在して、
が存在して、
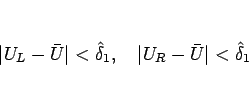
に対して、
(2.12) を
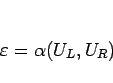
の形に書き表すことができる。これは 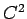 級であり、
級であり、
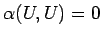 を満たす。
必要なら、
を満たす。
必要なら、
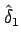 を少し小さく取って、
を少し小さく取って、
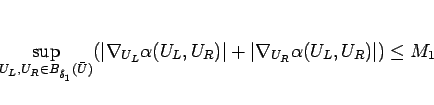 |
(2.15) |
とすることもできる。
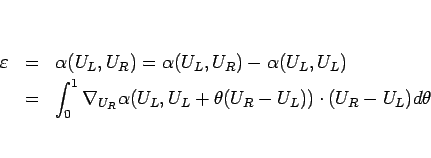
であるから、(2.13) より、
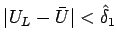 ,
,
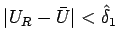 に対して
に対して
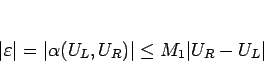 |
(2.16) |
と、
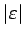 を
を 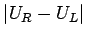 で評価できる。
で評価できる。
逆に、
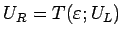 を考えると、ある
を考えると、ある
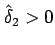 を取って
を取って
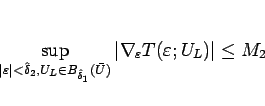 |
(2.17) |
とできるので、
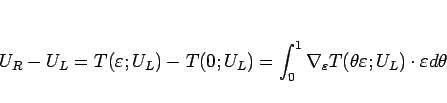
より、
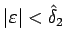 ,
,
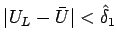 に対して
に対して
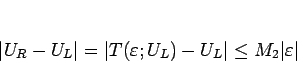 |
(2.18) |
となる。
しかし、
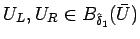 でも、
Riemann 問題の解 (の途中の値) は
でも、
Riemann 問題の解 (の途中の値) は
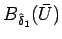 の中に収まるとは限らない。
解の途中の値は、
の中に収まるとは限らない。
解の途中の値は、
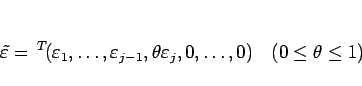
に対して
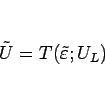
と表すことができる2。
このとき、(2.14), (2.16)
により、
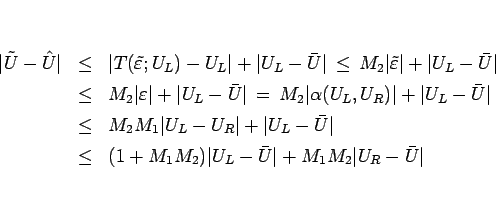
となるので、
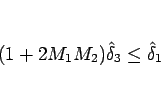 |
(2.19) |
となる
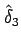 を取れば、
を取れば、
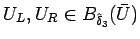 に対し
途中の解の値
に対し
途中の解の値
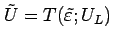 は
すべて
は
すべて
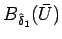 に収まることになる。
よって、その途中の値を初期値とするような Riemann 問題を再び解くことが
できることになる。
に収まることになる。
よって、その途中の値を初期値とするような Riemann 問題を再び解くことが
できることになる。
しかし、今度はその解が
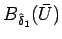 に収まる保証はないので、
これを繰り返していくには
(実際に Glimm の差分ではそのようなことを繰り返すのであるが)、
このような局所的な逐次評価だけでは無理で、
より大域的な評価、アプリオリな評価が必要になる。
に収まる保証はないので、
これを繰り返していくには
(実際に Glimm の差分ではそのようなことを繰り返すのであるが)、
このような局所的な逐次評価だけでは無理で、
より大域的な評価、アプリオリな評価が必要になる。
また、
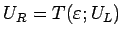 は
は
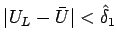 ,
,
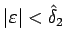 のとき、
のとき、
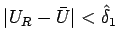 であるとは限らないので、
であるとは限らないので、
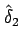 を少し小さくして、
を少し小さくして、
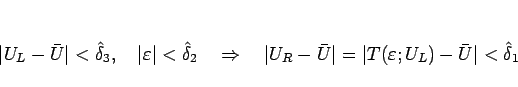
が成り立つようにしておく。これは (2.16) より、
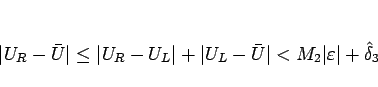
であるので、例えば
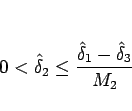 |
(2.20) |
としておけば可能である。
さらに、
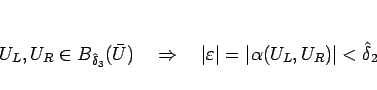
となるように
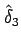 を取ることにする。
これは、(2.14) より、
を取ることにする。
これは、(2.14) より、
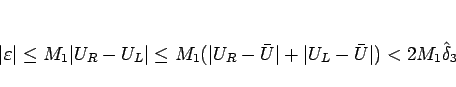
であるから、
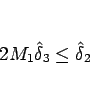 |
(2.21) |
であればよい。
ここで、
(2.18) と
(2.19) とから自然に
(2.17) が導かれるので、
結局
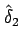 ,
,
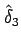 は
(2.18) と
(2.19) とを満たすように取ればよいことがわかる。
は
(2.18) と
(2.19) とを満たすように取ればよいことがわかる。
竹野茂治@新潟工科大学
2009年1月18日
![]() を、
を、
![]() を考えると、ある
を考えると、ある
![]() を取って
を取って
![]() でも、
Riemann 問題の解 (の途中の値) は
でも、
Riemann 問題の解 (の途中の値) は
![]() の中に収まるとは限らない。
解の途中の値は、
の中に収まるとは限らない。
解の途中の値は、
![]() に収まる保証はないので、
これを繰り返していくには
(実際に Glimm の差分ではそのようなことを繰り返すのであるが)、
このような局所的な逐次評価だけでは無理で、
より大域的な評価、アプリオリな評価が必要になる。
に収まる保証はないので、
これを繰り返していくには
(実際に Glimm の差分ではそのようなことを繰り返すのであるが)、
このような局所的な逐次評価だけでは無理で、
より大域的な評価、アプリオリな評価が必要になる。
![]() は
は
![]() ,
,
![]() のとき、
のとき、
![]() であるとは限らないので、
であるとは限らないので、
![]() を少し小さくして、
を少し小さくして、
![]() ,
,
![]() は
(2.18) と
(2.19) とを満たすように取ればよいことがわかる。
は
(2.18) と
(2.19) とを満たすように取ればよいことがわかる。