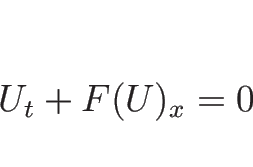 |
(A.118) |
不連続性を持つような一般的な関数に対して、それが方程式
一般に、![]() に対し、関数の集合
に対し、関数の集合 ![]() を
を
とし、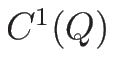
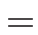
上定義された関数で、
上連続かつ微分可能で、 そのすべての 1 階 (偏) 導関数も
上連続あるもの全体の集合
と定める。ここで、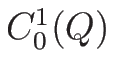
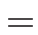
の関数で、その台が
上コンパクトであるもの 全体の集合
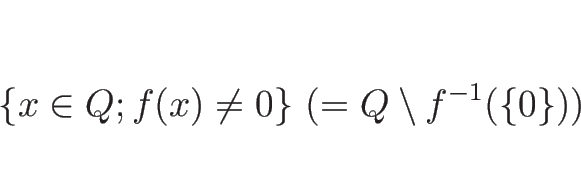
例えば、![]() ,
,
![]() のとき、
のとき、
![]() は、
は、![]() であれば
であれば
![]() 内でコンパクトである。
一方、
内でコンパクトである。
一方、
![]() は、(
は、(![]() の 相対位相に関して)
の 相対位相に関して)
![]() の 閉部分集合であるが、
この集合内の点列
の 閉部分集合であるが、
この集合内の点列
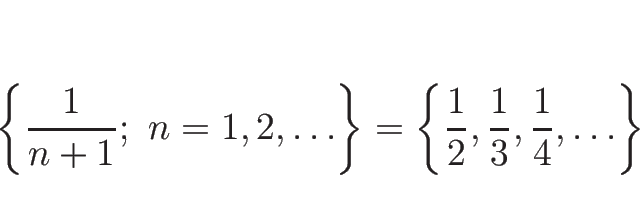
しかし、端が含まれてはいけない、というわけではなくて、例えば
![]() の場合には、
の場合には、![]() は
は
![]() のコンパクトな部分集合となる。
のコンパクトな部分集合となる。
つまり荒く言えば、コンパクトとは、
「有界 (無限に伸びていない) な
閉集合で、それを ![]() 全体の部分集合と見たときの境界まで
キッチリ
全体の部分集合と見たときの境界まで
キッチリ ![]() に含まれる部分集合」
となる。
に含まれる部分集合」
となる。
よって、
![]() の場合は、
の場合は、
![\begin{displaymath}
\mathop{\mathrm{supp}}\nolimits f\subset [a,b]\hspace{1zw}(0<a<b<1)
\end{displaymath}](img1282.png)
![\begin{displaymath}
\mathop{\mathrm{supp}}\nolimits g\subset [0,b]\hspace{1zw}(0<b<1)
\end{displaymath}](img1287.png)
以下の命題 A.1 のように、
集合 ![]() には十分多くの関数が含まれていることが知られている。
には十分多くの関数が含まれていることが知られている。
![]() が
が ![]() の開領域であるとき、
の開領域であるとき、
![]() が、任意の
が、任意の
![]() に対し、
に対し、
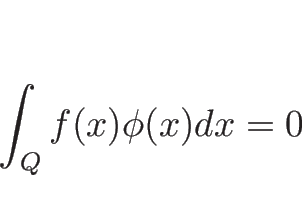
なお、
![]() であるとは、
であるとは、
![]() が
が ![]() 上ルベーグ可測な関数で、
上ルベーグ可測な関数で、
![]() 内の任意のコンパクト集合
内の任意のコンパクト集合 ![]() に対して
に対して
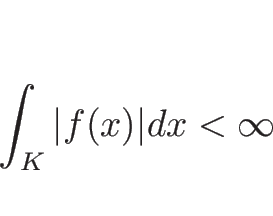
もし、![]() が
が ![]() でなく、どんな関数でもいいという条件ならば、
でなく、どんな関数でもいいという条件ならば、
![\begin{displaymath}
\phi(x)=
\left\{\begin{array}{ll}
\displaystyle \frac{f(x)}...
...eq 0$\ のとき})\\ [.5zh]
0 & (\mbox{その他})\end{array}\right.\end{displaymath}](img1297.png)
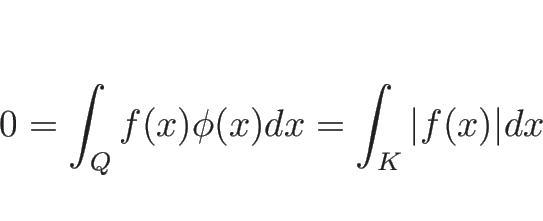
なお、命題 A.1 の証明には ルベーグ積分等の知識を必要とするので、ここではその証明は行わない。
さて、![]() が
が ![]() 平面
平面 ![]() の開領域であるとき、
の開領域であるとき、
![]() が、
が、![]() 上で
方程式 (A.1) の 弱解 (weak solution)
であるとは、任意の
上で
方程式 (A.1) の 弱解 (weak solution)
であるとは、任意の
![]() に対して、
に対して、
これは、少なくとも形式的には、
方程式 (A.1) に ![]() をかけて、
をかけて、
![]() 上で部分積分して得られる式である。
この式 (A.2) には、
上で部分積分して得られる式である。
この式 (A.2) には、
![]() や
や ![]() の微分は含まれていないので、
の微分は含まれていないので、
![]() が微分可能でない関数でも構わなくて、弱解にはなりうる。
が微分可能でない関数でも構わなくて、弱解にはなりうる。
又、もし ![]() が
が ![]() 上滑らかな (A.2) の解であれば、
上滑らかな (A.2) の解であれば、
![]() 上で
上で
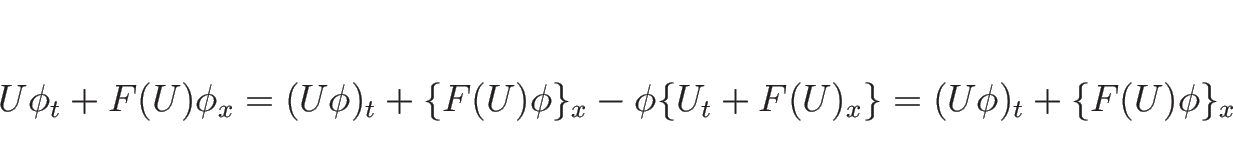
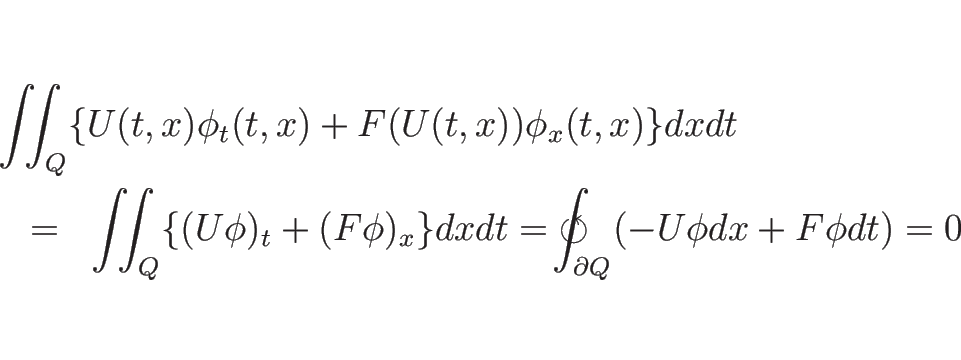
逆に、![]() が滑らかな関数で、かつ弱解、すなわち任意の
が滑らかな関数で、かつ弱解、すなわち任意の
![]() に対し (A.2) を満たせば、
に対し (A.2) を満たせば、
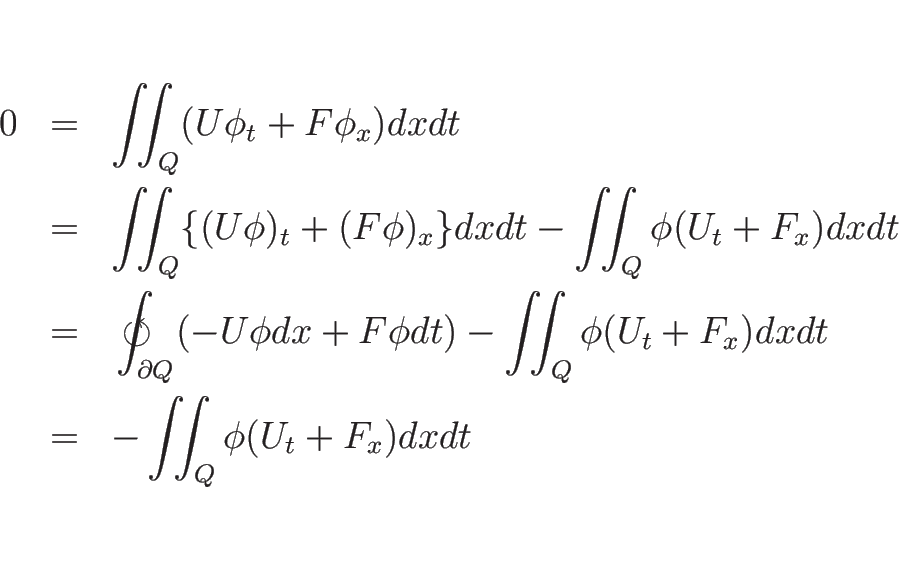
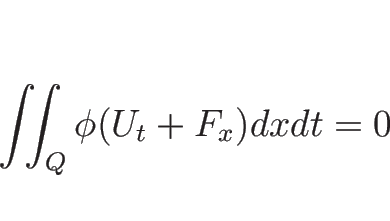
しかもこの議論は局所化ができ、
もし ![]() が弱解で、その一部分が滑らかであるならば、
その部分にだけ台を持つテスト関数に対して今の計算を行えばわかるが、
結局、その滑らかな部分ではやはり (A.1) を
満たすことになる。
つまり、弱解は滑らかな部分では必ず (A.1) を
満たす必要があることがわかる。
が弱解で、その一部分が滑らかであるならば、
その部分にだけ台を持つテスト関数に対して今の計算を行えばわかるが、
結局、その滑らかな部分ではやはり (A.1) を
満たすことになる。
つまり、弱解は滑らかな部分では必ず (A.1) を
満たす必要があることがわかる。
又、上の計算と 4.2 節の計算を
見比べるとわかるが、
![]() が弱解であり、不連続線
が弱解であり、不連続線 ![]() の両側で滑らかで
(よって (A.1) を満たし)、
の両側で滑らかで
(よって (A.1) を満たし)、
![]() では第一種不連続であるならば、
では第一種不連続であるならば、
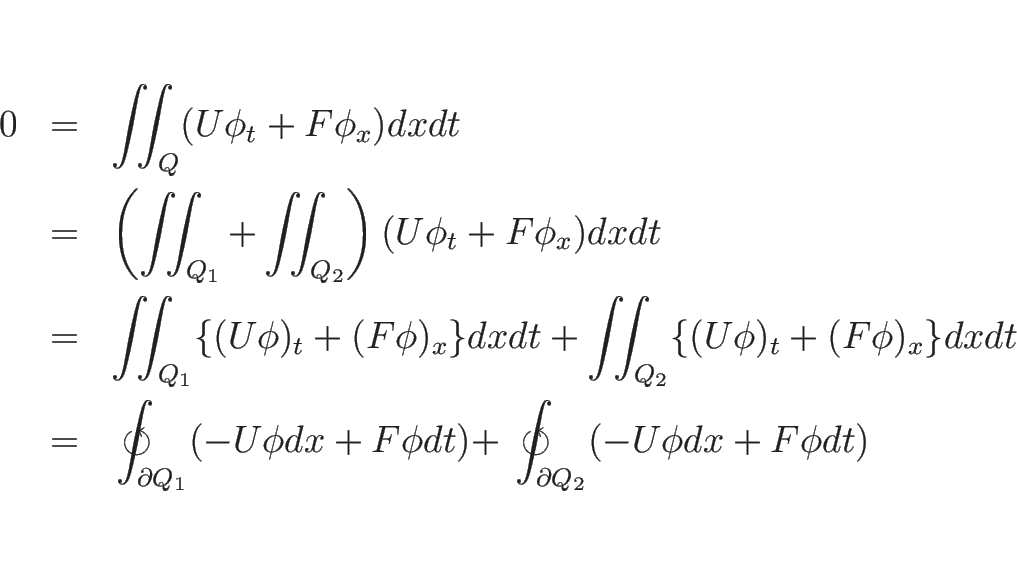
![\begin{eqnarray*}0
&=&
\int_{x=d(t)}(-U\phi d'(t)+F\phi dt)\Big\vert _{x=d(t)-...
...{x=d(t)+0}dt
\\ &=&
\int_{x=d(t)}\phi(t,d(t))\{[U]d'(t)-[F]\}dt\end{eqnarray*}](img1317.png)
![\begin{displaymath}[U]d'(t)=[F]
\end{displaymath}](img1318.png)
つまり、弱解は、
また、初期値問題
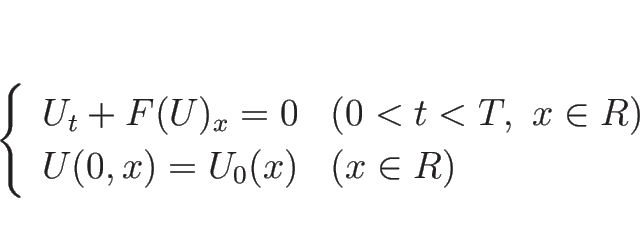
任意の
![]() に対し、
に対し、
なお、![]() は
は
![]() の関数となっているので、
の関数となっているので、
![]() での値
での値 ![]() は一般には (恒等的には) 0 ではない。
は一般には (恒等的には) 0 ではない。
この定義も (A.2) の場合と同様の性質を持ち、
滑らかで
![]() を持つ
を持つ
![]() がこの弱解の定義を満たすことは、
(A.1)、およびほとんどすべての
がこの弱解の定義を満たすことは、
(A.1)、およびほとんどすべての ![]() に対して
に対して
![]() を満たすことと同値であることが容易にわかる。
を満たすことと同値であることが容易にわかる。
本稿でこれまでに述べた膨張波や衝撃波、接触不連続、 およびそれらから構成されたリーマン問題の解は、 いずれも (A.3) を満たす弱解になっている。
ただし、これらの弱解の定義には 4.7 節で述べた ラックス条件のようなものは含まれないので、 物理的に認められない膨張衝撃波のようなものまで含まれてしまうし、 解の一意性が保証されない。 しかし、ラックス条件は、不連続性が第一種不連続な衝撃波として 明確に現われる部分でしか設定できないので、 一般の弱解に対してその条件を設定することは困難である。
よって、一般の弱解から物理的に意味のある弱解のみを選択するために、 ラックス条件に代わる何らかの条件を課す必要があるが、 それが B 節で与える エントロピー条件と呼ばれるものである。
竹野茂治@新潟工科大学