4.10 バロトロピックのオイラー座標系の場合
次はバロトロピックオイラー座標系の場合の方程式
(2.10), (2.15) (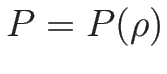 ,
, 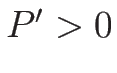 ) を考える。
この場合は、ランキン-ユゴニオ条件は
) を考える。
この場合は、ランキン-ユゴニオ条件は
であるから、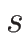 を消去すると
を消去すると
となり、
であるから、
よって、
となる。
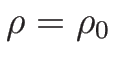 でのテイラー展開を利用すると、
でのテイラー展開を利用すると、
となるので、
となる。なお、この微分の値は、
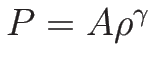 ,
, 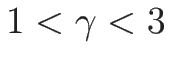 の場合は、
の場合は、
となるので負となる。
よって、
となる。よって、
とすると、
となるので、
であることがわかる。よって、
によって 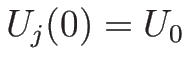 ,
,
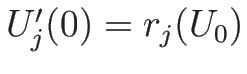 となる。
となる。
さらに、
であり、
となるので、
であるから、
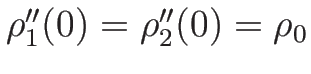 であれば、
であれば、
となる。
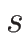 は、
は、
であるから、
となり、確かに
となる。
この場合、
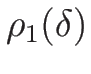 ,
,
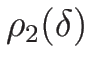 としては、例えば
としては、例えば
と取ればよい。
竹野茂治@新潟工科大学
2018-08-01
![\begin{displaymath}
\begin{array}{l}
s[\rho]=[\rho u],\\
s[\rho u]=[\rho u^2+P(\rho)]
\end{array}\end{displaymath}](img925.png)
![\begin{displaymath}[\rho u]^2=[\rho][\rho u^2+P]
\end{displaymath}](img926.png)
![\begin{displaymath}[\rho u]^2-[\rho][\rho u^2]=\rho_0\rho[u]^2
\end{displaymath}](img793.png)
![\begin{displaymath}[u]
=\pm\sqrt{\frac{[\rho][P]}{\rho_0\rho}}
=\pm\sqrt{\frac{(\rho-\rho_0)(P(\rho)-P(\rho_0))}{\rho_0\rho}}
\end{displaymath}](img927.png)
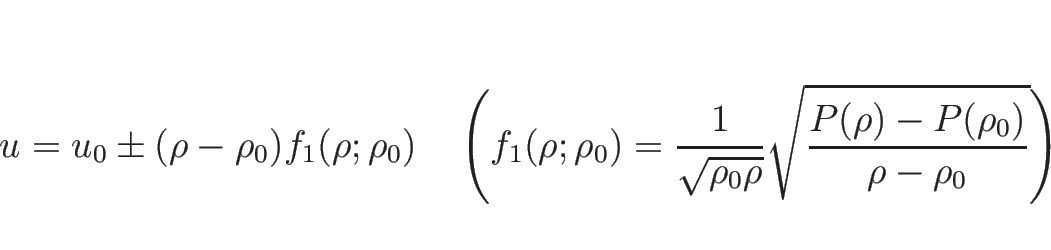
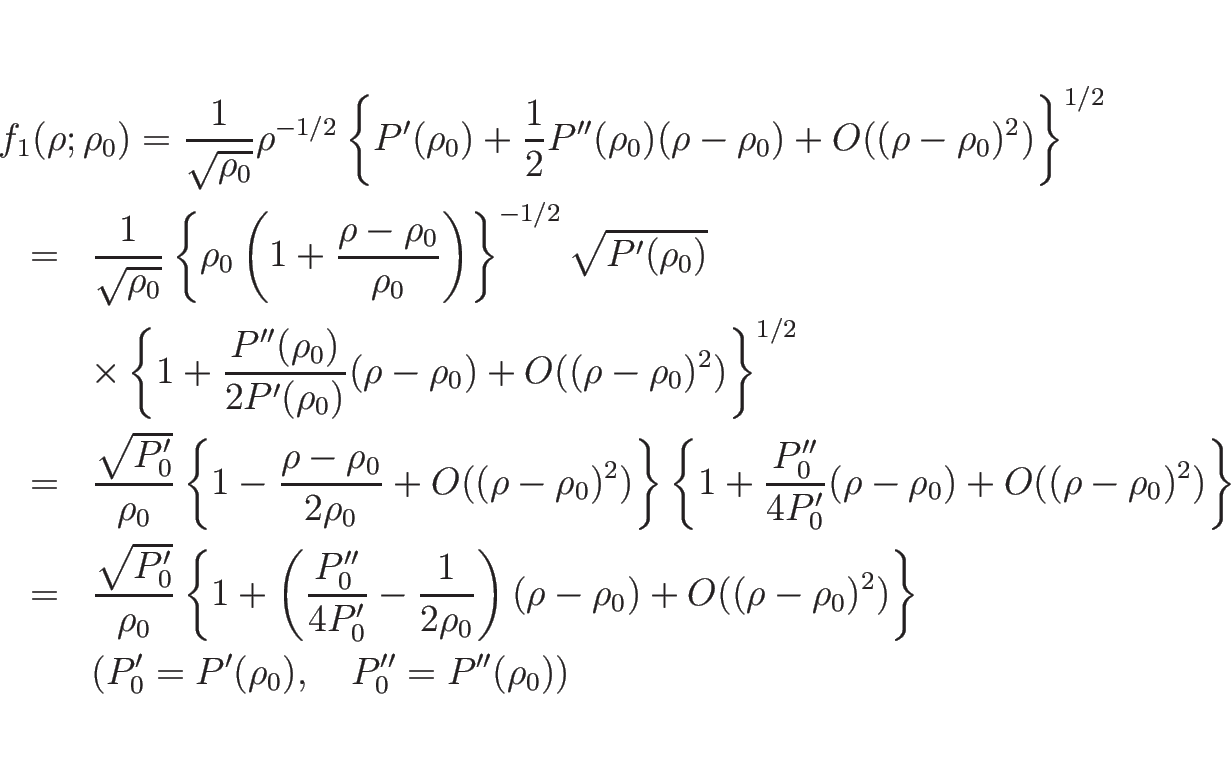
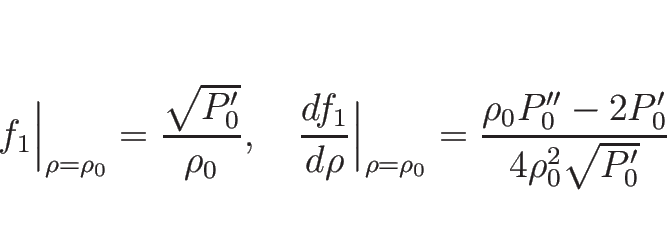
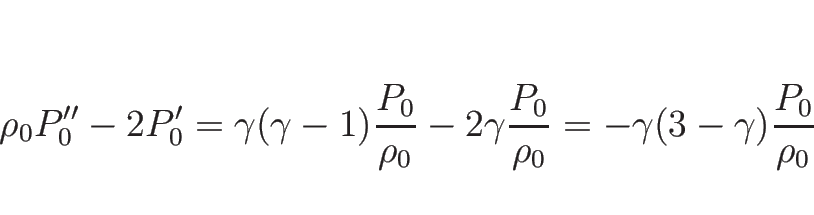
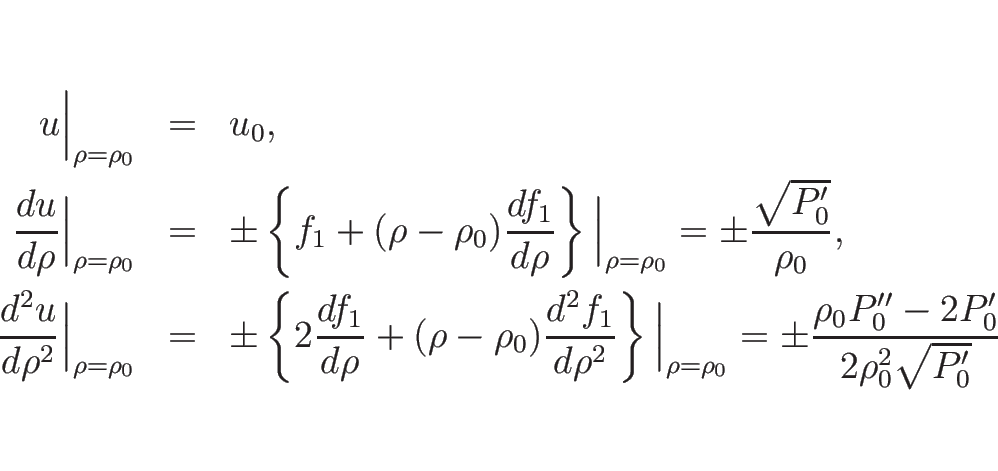
![\begin{displaymath}
V_{\pm}(\rho)
=\left[\begin{array}{c}\rho\\ u\end{array}\rig...
...c}\rho\\ u_0\pm(\rho-\rho_0)f_1(\rho;\rho_0)\end{array}\right]
\end{displaymath}](img934.png)
![\begin{displaymath}
V_{\pm}'(\rho_0)
=\left[\begin{array}{c}1\\ \pm\sqrt{P'_0}/\...
...left[\begin{array}{c}\pm\rho_0\\ \sqrt{P'_0}\end{array}\right]
\end{displaymath}](img935.png)
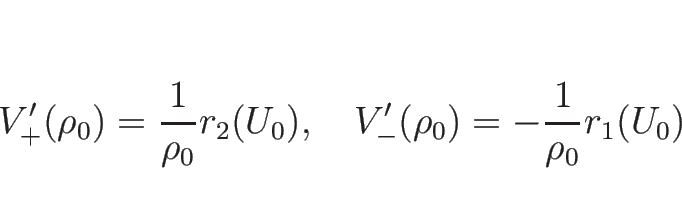
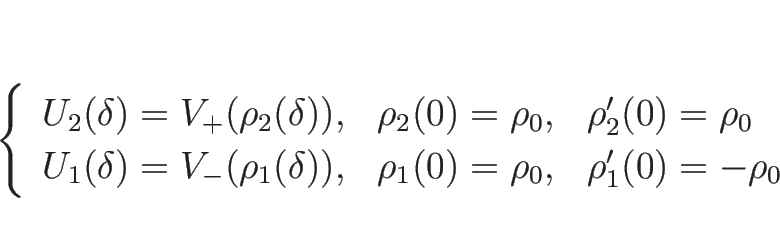
![\begin{displaymath}
V_{\pm}''(\rho_0)=\left[\begin{array}{c}0\\ \pm(\rho_0P''_0-2P'_0)/(2\rho_0^2\sqrt{P'_0})\end{array}\right]
\end{displaymath}](img940.png)
![\begin{eqnarray*}\nabla_Ur_1\cdot r_1
&=&
\nabla_U\left[\begin{array}{c}-\rho\...
...ft[\begin{array}{c}\rho\\ \rho P''/(2\sqrt{P'})\end{array}\right]\end{eqnarray*}](img941.png)
![\begin{eqnarray*}\lefteqn{(\nabla_U r_1\cdot r_1+r_1)(U_0)
=
\left[\begin{arra...
...'_0)/(2\sqrt{P'_0})\end{array}\right]
=
\rho_0^2V_{+}''(\rho_0)\end{eqnarray*}](img942.png)
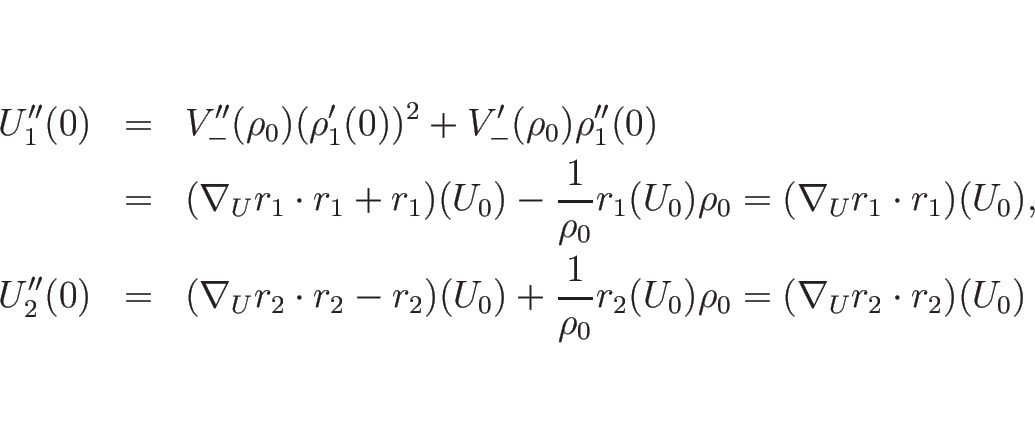
![]() は、
は、
![\begin{displaymath}
s
=
\frac{[\rho u]}{[\rho]}
=
\frac{\rho[u]+u_0[\rho]}{[\rho]}
=
u_0+\rho\frac{[u]}{[\rho]}
=
u_0\pm \rho f_1(\rho;\rho_0)
\end{displaymath}](img945.png)
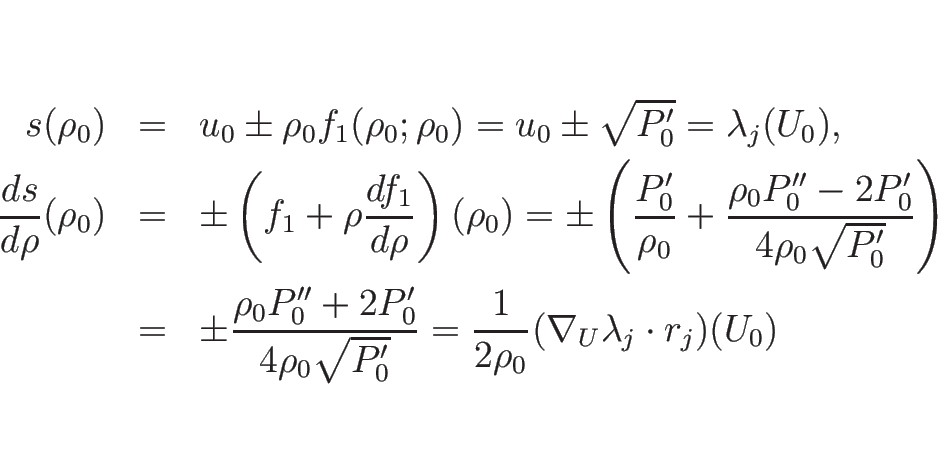
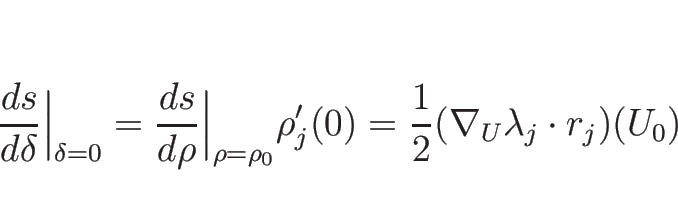
![]() ,
,
![]() としては、例えば
としては、例えば