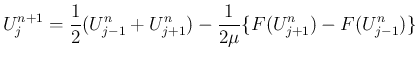 (10)
(10)
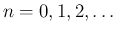 で、
で、
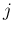 は通常
は通常 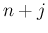 が奇数のもののみを考える。
また、
が奇数のもののみを考える。
また、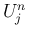 は (3) の解
は (3) の解 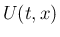 の
の
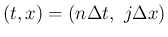 での値を近似するもの (
での値を近似するもの (
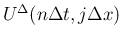 ) であり、
よって (10) は、微分方程式 (3) を
) であり、
よって (10) は、微分方程式 (3) を
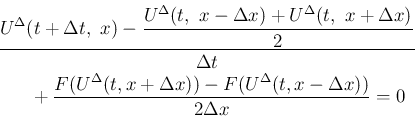
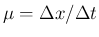 )。
)。
以後、(10) の右辺の式を、
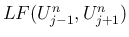 , あるいは
, あるいは
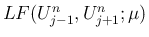 と
書くこととする:
と
書くこととする:
LF 差分の 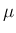 には、安定性のため通常 CFL 条件
(Courant-Friedrichs-Lewy 条件):
には、安定性のため通常 CFL 条件
(Courant-Friedrichs-Lewy 条件):
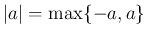 なので、
なので、
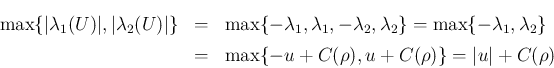
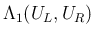 は、
と書ける。
は、
と書ける。
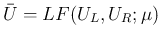 の
の 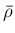 は、
は、
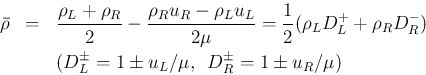
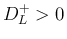 ,
, 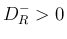 となるので、
これにより
となるので、
これにより 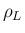 ,
, 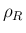 の両方が 0 でない限り
の両方が 0 でない限り 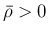 となることが保証される。
となることが保証される。
竹野茂治@新潟工科大学