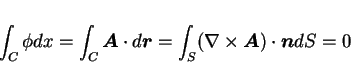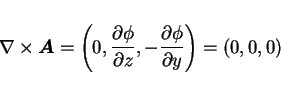

Next: 4 最後に
Up: 講義の補足 (2004 前期)
Previous: 2 任意の範囲での積分が 0
(PDF ファイル: hosoku1.pdf)
前節と同じ論法で、
2., 4. を
次のように変えても同様の事実が成り立つ。
定理 2
- どんな領域の境界面
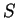 (閉曲面) に対しても
(閉曲面) に対しても
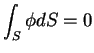 ならば
ならば 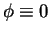
- どんな曲面の境界線
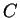 (閉曲線) に対しても
(閉曲線) に対しても
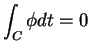 ならば
ならば 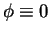 (
(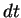 の積分でなく、
の積分でなく、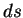 の積分でも同じことが言える)
の積分でも同じことが言える)
しかし、例えばこの 8. は、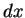 や
や
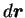 の積分ではもはや成り立たない。それは、例えば
の積分ではもはや成り立たない。それは、例えば
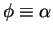 (= 0 ではない定数) の場合、
(= 0 ではない定数) の場合、
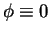 ではないが、
任意の閉曲線に対して
ではないが、
任意の閉曲線に対して
(閉曲線なので 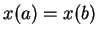 ) となってしまうからである。
) となってしまうからである。
つまり、「閉」曲線に関する積分の場合、
その任意性は 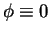 が言えてしまう程のものではないこともある。
それはベクトル場に対しても同様であり、
例えば以下の条件が満たされても
が言えてしまう程のものではないこともある。
それはベクトル場に対しても同様であり、
例えば以下の条件が満たされても 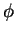 ,
,
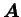 は 0 (や
は 0 (や
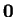 )
であるとは限らない。
)
であるとは限らない。
- どんな曲面の境界線
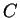 (閉曲線) に対しても
(閉曲線) に対しても
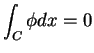
- どんな領域の境界面
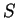 (閉曲面) に対しても
(閉曲面) に対しても
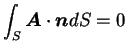
- どんな曲面の境界線
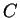 (閉曲線) に対しても
(閉曲線) に対しても
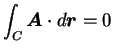
では、9.,
10.,
11.,
の元ではどこまで言えるかを考えてみる。
例えば 10. の条件の元では、
その領域を 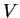 とすると、発散定理によりその
とすると、発散定理によりその 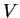 に対して
に対して
が言えることになる。よって 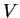 の任意性と 1. により
の任意性と 1. により
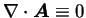 が成り立つ。
が成り立つ。
同様に、11. の元では、その曲面を 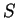 とすると
ストークスの公式により
とすると
ストークスの公式により
が言える。よって 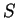 の任意性と 3. により
の任意性と 3. により
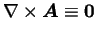 が成り立つ。
が成り立つ。
9. の場合は、
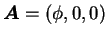 と考えれば
と考えれば
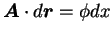 なので、再びストークスの公式により
なので、再びストークスの公式により
より 1. から
となり、よって
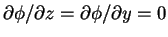 より
より
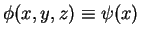 (
(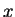 のみの 1 変数関数)
となることが分かる。
のみの 1 変数関数)
となることが分かる。
命題 3
- 9. ならば
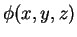 は
は
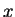 のみの関数
のみの関数
- 10. ならば
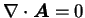
- 11. ならば
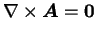
もちろんこれらは逆も成立する。


Next: 4 最後に
Up: 講義の補足 (2004 前期)
Previous: 2 任意の範囲での積分が 0
Shigeharu TAKENO
2004年 7月 29日
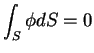 ならば
ならば 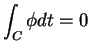 ならば
ならば ![]() や
や
![]() の積分ではもはや成り立たない。それは、例えば
の積分ではもはや成り立たない。それは、例えば
![]() (= 0 ではない定数) の場合、
(= 0 ではない定数) の場合、
![]() ではないが、
任意の閉曲線に対して
ではないが、
任意の閉曲線に対して
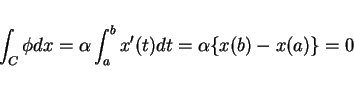
![]() が言えてしまう程のものではないこともある。
それはベクトル場に対しても同様であり、
例えば以下の条件が満たされても
が言えてしまう程のものではないこともある。
それはベクトル場に対しても同様であり、
例えば以下の条件が満たされても ![]() ,
,
![]() は 0 (や
は 0 (や
![]() )
であるとは限らない。
)
であるとは限らない。
![]() とすると、発散定理によりその
とすると、発散定理によりその ![]() に対して
に対して
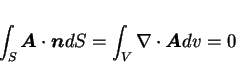
![]() とすると
ストークスの公式により
とすると
ストークスの公式により
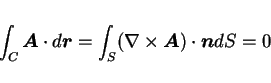
![]() と考えれば
と考えれば
![]() なので、再びストークスの公式により
なので、再びストークスの公式により