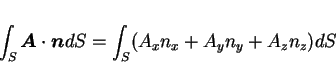

Next: 3 閉曲面、閉曲線の場合
Up: 講義の補足 (2004 前期)
Previous: 1 はじめに
(PDF ファイル: hosoku1.pdf)
任意の範囲での積分が 0 ならば被積分関数自体が 0 になる、
という事実がいくつか成り立つ。
定理 1
連続なスカラー場 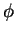 , ベクトル場
, ベクトル場
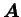 に対して次がいえる。
に対して次がいえる。
- どんな 3 次元領域
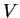 に対しても
に対しても
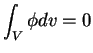 ならば
ならば 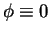
- どんな曲面
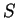 に対しても
に対しても
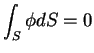 ならば
ならば 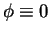
- どんな曲面
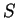 に対しても
に対しても
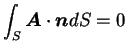 ならば
ならば
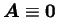
- どんな曲線
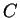 に対しても
に対しても
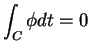 ならば
ならば 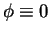
(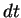 の積分でなく、
の積分でなく、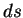 や
や 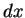 の積分などでも同じことが言える)
の積分などでも同じことが言える)
- どんな曲線
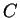 に対しても
に対しても
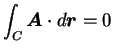 ならば
ならば
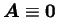
これらはいずれも、1 次元の場合の、
- 任意の
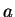 ,
,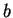 (
(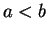 ) に対して
) に対して
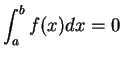 ならば
ならば 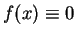
と同様の方針で証明される。
この 6. は、「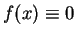 ではないとしたら、
ではないとしたら、
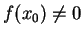 となる点
となる点 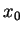 が少なくとも一つあり
(例えば
が少なくとも一つあり
(例えば 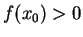 とする)、
とする)、
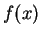 が連続ならばその
が連続ならばその 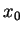 の近くの
の近くの 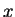 ではやはり正になるので、
その
ではやはり正になるので、
その 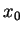 の近くで積分すれば正の値になるはずなので矛盾」
のように証明される。
の近くで積分すれば正の値になるはずなので矛盾」
のように証明される。
なお、3., 5. は
一見同様ではないようにも見えるが、例えば 3. は
なので、例えば 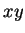 平面に平行な面を取れば
平面に平行な面を取れば 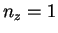 ,
, 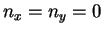 となり、
そこから
となり、
そこから 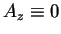 が導かれ、
他の成分
が導かれ、
他の成分 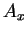 ,
, 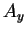 も
も 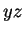 平面、
平面、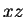 平面に平行な面を考えることで
同様に 0 となることが言える。
平面に平行な面を考えることで
同様に 0 となることが言える。


Next: 3 閉曲面、閉曲線の場合
Up: 講義の補足 (2004 前期)
Previous: 1 はじめに
Shigeharu TAKENO
2004年 7月 29日
![]() , ベクトル場
, ベクトル場
![]() に対して次がいえる。
に対して次がいえる。
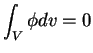 ならば
ならば 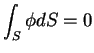 ならば
ならば 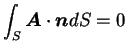 ならば
ならば
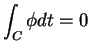 ならば
ならば 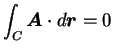 ならば
ならば
![]() ではないとしたら、
ではないとしたら、
![]() となる点
となる点 ![]() が少なくとも一つあり
(例えば
が少なくとも一つあり
(例えば ![]() とする)、
とする)、
![]() が連続ならばその
が連続ならばその ![]() の近くの
の近くの ![]() ではやはり正になるので、
その
ではやはり正になるので、
その ![]() の近くで積分すれば正の値になるはずなので矛盾」
のように証明される。
の近くで積分すれば正の値になるはずなので矛盾」
のように証明される。