

Next: 9 数値計算結果
Up: 斜円錐の側面積について
Previous: 7 この積分の計算可能性
(PDF ファイル: yokoyama1.pdf)
8 根号内が完全平方になる場合
7 節で述べたように、
一般には (17) を簡単な式で表すことはできないが、
根号の中が完全平方式である場合は簡単に計算できる式になる。
この節では、まずその条件を考えてみることにする。
式 (17) の完全平方性を考える場合、以下の 2 つの考え方がある。
- (17) の根号の内部が直接
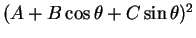 になる場合
になる場合
- (17) を
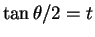 と置換したときの
根号内の
と置換したときの
根号内の 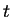 の 4 次式が
の 4 次式が
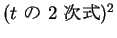 になる場合
になる場合
しかし容易に分かるようにこの両者は同等である
(一方が成り立てば他方も成り立つ) ので、
どちらか一方のみを考えれば良い。
いずれにしても恒等式を考えるわけだが、前者は関数
の一次独立性を、後者は
の一次独立性を用いて両辺の係数比較を行なうことになる。
今回は前者の三角関数を使った計算で考えることにする。
まず、
と置いて両辺を展開して整理する。倍角の公式を用いると
となるので、係数比較して次の式を得る。
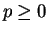 ,
, 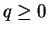 ,
, 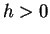 ,
, 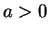 ,
, 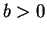 として、
これらの式が成り立つ (つまり完全平方になる) ために
として、
これらの式が成り立つ (つまり完全平方になる) ために
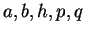 が満たす条件を求め、そのときの
が満たす条件を求め、そのときの 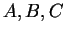 を求めることが目標である。
を求めることが目標である。
まず、(21) より、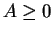 として構わないことに注意する。
として構わないことに注意する。
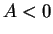 の場合は
の場合は 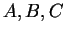 をすべて
をすべて 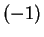 倍すれば同じことになる。
倍すれば同じことになる。
(23)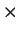 (24)
(24)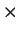 (26)
より
(26)
より
となるので、もし 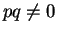 ならば、(26) より
ならば、(26) より 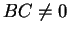 なので、この式を (26) の 2 乗で割ると
なので、この式を (26) の 2 乗で割ると 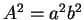 ,
よって
,
よって 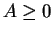 より
より 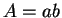 を得る。よって
を得る。よって 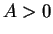 なので、
(23), (24) より
なので、
(23), (24) より
となる。しかし、これらを (22) に代入すると、
となるが、これは 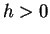 ,
, 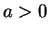 ,
, 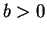 に矛盾する。
よって、
に矛盾する。
よって、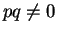 のときは完全平方にはなりえないことが分かる。
のときは完全平方にはなりえないことが分かる。
今度は 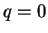 とすると、(24), (26) より
とすると、(24), (26) より
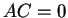 ,
, 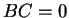 なので、もし
なので、もし 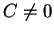 ならば
ならば 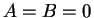 となり、
(23) より
となり、
(23) より 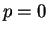 となる。ところがこの場合も
(22)
となる。ところがこの場合も
(22)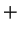 (25) を考えると、
(25) を考えると、
となり、これも 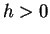 ,
, 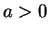 ,
, 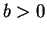 に矛盾するので、
に矛盾するので、
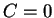 でなければならない。
でなければならない。
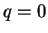 ,
, 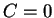 を (22), (25) に代入すると
を (22), (25) に代入すると
より、
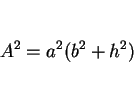 |
(27) |
となる。この 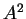 と
と 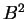 を (23) の 2 乗に代入したものが
完全平方のための条件となる。代入して展開、整理すると
を (23) の 2 乗に代入したものが
完全平方のための条件となる。代入して展開、整理すると
となる。
この最後の式は 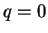 と合わせて、4 節で求めた、
この図形が直円錐の一部となる条件 (16) (
と合わせて、4 節で求めた、
この図形が直円錐の一部となる条件 (16) (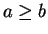 )
に等しい。
)
に等しい。
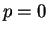 としたときも同様に
としたときも同様に 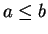 のときの直円錐の一部になる条件が
得られる。
のときの直円錐の一部になる条件が
得られる。
さて、このとき
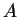 は (27) より
は (27) より
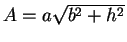 (
(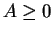 ) であり、
) であり、
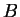 は (23) と (28) より、
は (23) と (28) より、
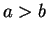 ,
, 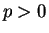 のときは (
のときは (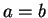 ,
, 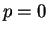 のときは単なる直円錐になる)、
のときは単なる直円錐になる)、
となるので、(21) の右辺のカッコの中は
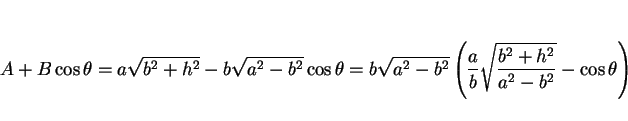 |
(29) |
となる。ここで、
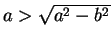 ,
,
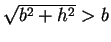 なので、
なので、
となり、(29) は正の値となる。
結局この場合は、公式 (17) は
となるので、これを計算すれば
となる。
この最後の式は、通常の直円錐の場合の公式 (1) に
よく似た式となっているが、
つまり直円錐の一部の場合には綺麗な性質が成り立つ、ということを意味する。
以上をまとめると、4 節で考察したように、
この図形が直円錐の一部になる場合には、
となることになる。
この、直円錐の一部になる場合以外にも
 が楕円積分にならない場合があるかも知れないが、
それは今のところは不明である。
が楕円積分にならない場合があるかも知れないが、
それは今のところは不明である。


Next: 9 数値計算結果
Up: 斜円錐の側面積について
Previous: 7 この積分の計算可能性
Shigeharu TAKENO
2005年 2月 28日
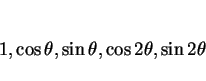
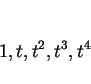
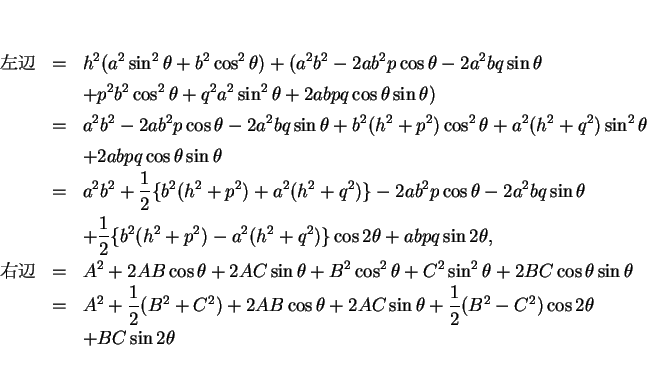
![]() として構わないことに注意する。
として構わないことに注意する。
![]() の場合は
の場合は ![]() をすべて
をすべて ![]() 倍すれば同じことになる。
倍すれば同じことになる。
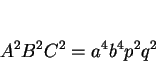
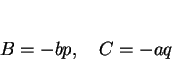
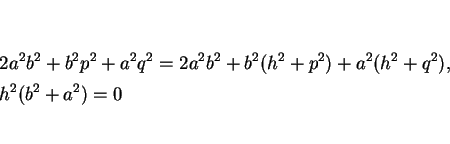
![]() とすると、(24), (26) より
とすると、(24), (26) より
![]() ,
, ![]() なので、もし
なので、もし ![]() ならば
ならば ![]() となり、
(23) より
となり、
(23) より ![]() となる。ところがこの場合も
(22)
となる。ところがこの場合も
(22)![]() (25) を考えると、
(25) を考えると、
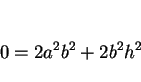
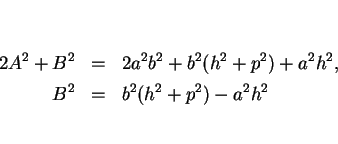
![]() は (27) より
は (27) より
![]() (
(![]() ) であり、
) であり、
![]() は (23) と (28) より、
は (23) と (28) より、
![]() ,
, ![]() のときは (
のときは (![]() ,
, ![]() のときは単なる直円錐になる)、
のときは単なる直円錐になる)、
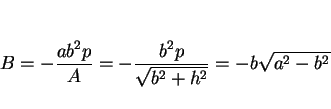
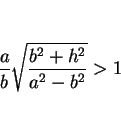
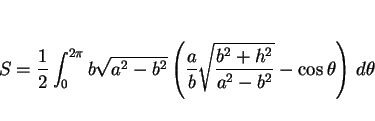
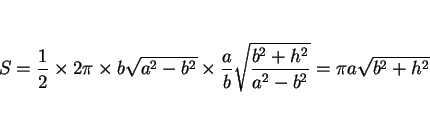
![]() が楕円積分にならない場合があるかも知れないが、
それは今のところは不明である。
が楕円積分にならない場合があるかも知れないが、
それは今のところは不明である。