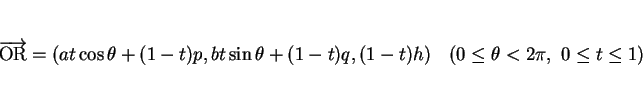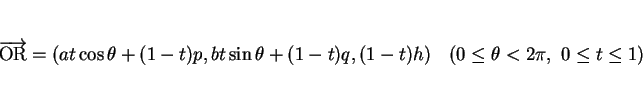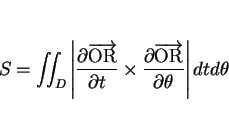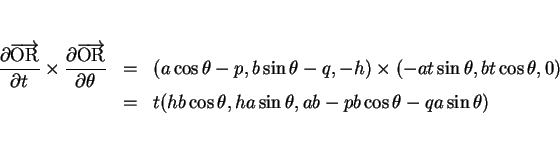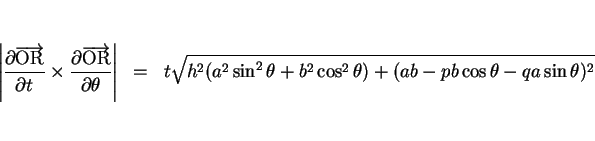

Next: 6 曲面積を求める公式:
Up: 斜円錐の側面積について
Previous: 4 問題の図形が直円錐の一部になる条件
(PDF ファイル: yokoyama1.pdf)
5 曲面積を求める公式: その 1
この節では、2 節で述べた方針 2. に
従って、曲面積 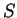 を表す式を求める。
を表す式を求める。
であるので、これを曲面積の公式
に代入する。
なので、
となり、
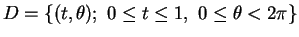 より
より
となる。


Next: 6 曲面積を求める公式:
Up: 斜円錐の側面積について
Previous: 4 問題の図形が直円錐の一部になる条件
Shigeharu TAKENO
2005年 2月 28日