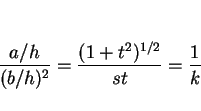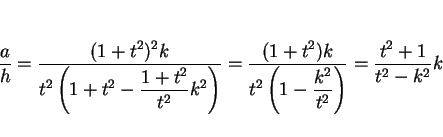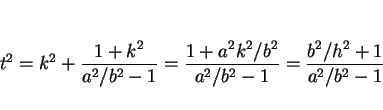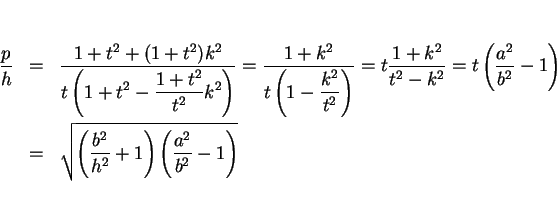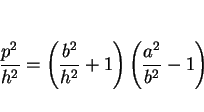

Next: 5 曲面積を求める公式:
Up: 斜円錐の側面積について
Previous: 3 問題の定式化
(PDF ファイル: yokoyama1.pdf)
4 問題の図形が直円錐の一部になる条件
3 節で問題を定式化したが、
底面を一般の楕円に拡張し頂点の位置も一般の位置にしたので、
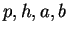 がなんらかの条件を満たせばこの図形
(斜楕円錐とでもいうべきものか) は直円錐を斜めに切ったものになる。
この節では、元の問題とは直接は関係ないが、その条件を導くことにする。
がなんらかの条件を満たせばこの図形
(斜楕円錐とでもいうべきものか) は直円錐を斜めに切ったものになる。
この節では、元の問題とは直接は関係ないが、その条件を導くことにする。
その条件を求めるには、なんとなく以下のような考え方でできそうに
見えるかも知れない:
原点 O を通り中心線 OP に垂直な平面 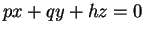 による
この曲面の断面を考えて、それが円になる条件を考える
(例えば原点からの距離が一定など)
による
この曲面の断面を考えて、それが円になる条件を考える
(例えば原点からの距離が一定など)
実は私も最初はこの方針で考えたのであるが、しかしこれは正しくない。
それは、もしこの図形が直円錐の一部である場合でもその 中心線 は、
その断面である楕円の中心 (今の場合原点 O) を通るとは限らないからである。
よって、中心線が決まらない状態ではこちらからのアプローチは難しいので、
逆に実際の直円錐の断面になる楕円を求め、それを当てはめてみることにする。
容易に分かるように、この図形が直円錐の一部である場合、
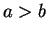 ならば頂点 P は
ならば頂点 P は 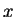 軸の真上、よって
軸の真上、よって 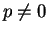 ,
, 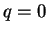
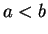 ならば頂点 P は
ならば頂点 P は 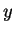 軸の真上、よって
軸の真上、よって 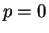 ,
, 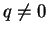
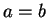 ならば頂点 P は原点の真上、よって
ならば頂点 P は原点の真上、よって 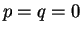
であるので、ここでは 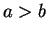 でかつ
でかつ 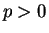 の場合を考える。
これが分かれば、
の場合を考える。
これが分かれば、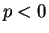 の場合は
の場合は 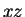 平面に関して対称になるだけ
(
平面に関して対称になるだけ
(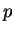 の変わりに
の変わりに 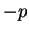 を取ればいい) だし、
を取ればいい) だし、
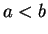 の場合は、
の場合は、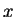 軸と
軸と 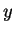 軸を入れ換える、すなわち
軸を入れ換える、すなわち
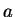 と
と 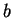 を入れ換えて、
を入れ換えて、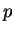 と
と 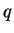 を入れ換えればよい。
を入れ換えればよい。
まず、図全体を 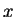 軸方向に平行移動して
直円錐の中心線が原点を通るようにし、
このときの P の移動先を
軸方向に平行移動して
直円錐の中心線が原点を通るようにし、
このときの P の移動先を
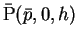 とする。
この場合、直円錐の中心線
とする。
この場合、直円錐の中心線
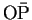 に垂直な平面
に垂直な平面
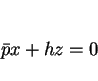 |
(4) |
による断面は原点中心の円であり、
これを円 C と呼びその半径を 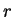 とする。
求めるものは、この直円錐の
とする。
求めるものは、この直円錐の 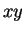 平面によって切り取られる楕円の方程式であり、
これは、
平面によって切り取られる楕円の方程式であり、
これは、
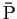 から円 C に光を当てたときに
から円 C に光を当てたときに 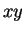 平面にできる影、
と見ることもできる (図 7)。
平面にできる影、
と見ることもできる (図 7)。
図 7:
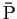 の円の影としての楕円
の円の影としての楕円
|
|
円 C 上の点は原点からの距離が 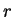 であるので
であるので
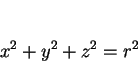 |
(5) |
を満たす。よって、(4), (5) より、
| |
|
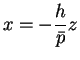 |
(6) |
| |
|
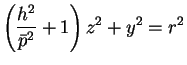 |
(7) |
が得られる。この円 C 上の点
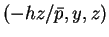 と頂点
と頂点 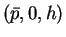 とを結ぶ直線と
とを結ぶ直線と 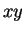 平面との交点
平面との交点 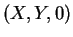 は
外分の公式より
は
外分の公式より
であるから、よって
となる。ここで、
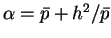 とおくと
とおくと
なので、
となるので、これを (7) に代入し整理すると、
となる。
円 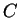 は傾き
は傾き 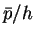 で傾いているので
その高さは
で傾いているので
その高さは
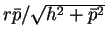 であり、
この高さよりも頂点
であり、
この高さよりも頂点 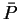 が高くないと直円錐と
が高くないと直円錐と 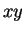 平面の交曲線は
楕円にはならない。よって、
平面の交曲線は
楕円にはならない。よって、
という条件が必要になる。この条件より
となるので、この場合は確かに (8) は楕円を表す。
なお、
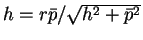 の場合、
すなわち円錐の母線と
の場合、
すなわち円錐の母線と 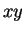 平面が平行になる場合は
平面が平行になる場合は
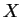 に関して 1 次、
に関して 1 次、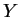 に関して 2 次式になるので放物線に、
に関して 2 次式になるので放物線に、
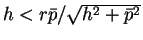 の場合は
の場合は
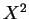 の係数と
の係数と 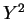 の係数が異なり双曲線となる。
の係数が異なり双曲線となる。
(8) を
の形に変形する。計算を見やすくするために、
として、後で消去すべき係数 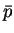 ,
, 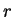 を
を 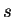 ,
, 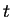 で置き換える。
で置き換える。
となるので、これらを (8) に代入して整理すると
となる。よって、
が得られる。
この図全体を 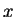 軸方向に
軸方向に 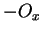 平行移動した場合に、
この楕円と光源である
平行移動した場合に、
この楕円と光源である
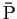 が
が
に移ると考えると、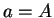 ,
, 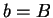 で
で
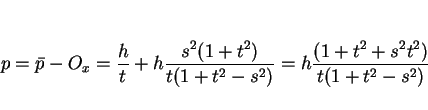 |
(12) |
となる。
これで、直円錐の一部である場合に 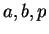 が
が 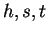 で
どのように表されるかが得られたことになるが、
逆に考えれば、
この
で
どのように表されるかが得られたことになるが、
逆に考えれば、
この 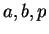 の式 (10), (11), (12)
から
の式 (10), (11), (12)
から 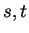 を消去して得られるのが、
元の図形が直円錐の一部となるための条件式、ということになる。
その条件式を以下で求める。
を消去して得られるのが、
元の図形が直円錐の一部となるための条件式、ということになる。
その条件式を以下で求める。
まず (10), (11) より、
と置くと、
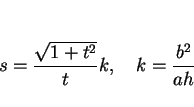 |
(13) |
となる。これを (10) に代入すると
より、
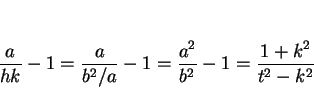 |
(14) |
となる。よって
より
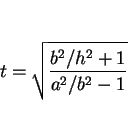 |
(15) |
となる。
(13) を (12) に代入すると、
(14), (15) より
が得られ、よって
ゆえに
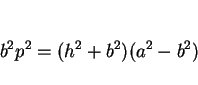 |
(16) |
が求める条件式になる。つまり、直円錐の一部になる条件は
となる。
なお、この条件 (16) の導出の途中の計算の複雑さに対して
最後の結果 (16) は割とやさしい式になるので、
何らかの幾何学的な性質を利用するようなもっと簡単に求める方法も
あるのかもしれない。


Next: 5 曲面積を求める公式:
Up: 斜円錐の側面積について
Previous: 3 問題の定式化
Shigeharu TAKENO
2005年 2月 28日
による この曲面の断面を考えて、それが円になる条件を考える (例えば原点からの距離が一定など)
![]() 軸方向に平行移動して
直円錐の中心線が原点を通るようにし、
このときの P の移動先を
軸方向に平行移動して
直円錐の中心線が原点を通るようにし、
このときの P の移動先を
![]() とする。
この場合、直円錐の中心線
とする。
この場合、直円錐の中心線
![]() に垂直な平面
に垂直な平面
![]() であるので
であるので
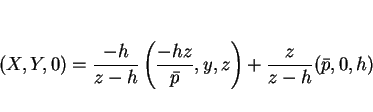
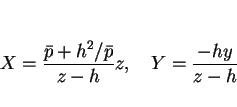
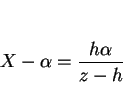
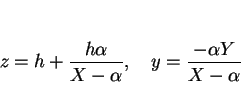
![]() は傾き
は傾き ![]() で傾いているので
その高さは
で傾いているので
その高さは
![]() であり、
この高さよりも頂点
であり、
この高さよりも頂点 ![]() が高くないと直円錐と
が高くないと直円錐と ![]() 平面の交曲線は
楕円にはならない。よって、
平面の交曲線は
楕円にはならない。よって、
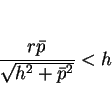
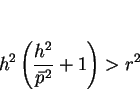
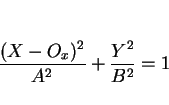
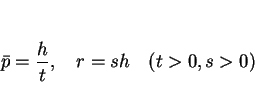
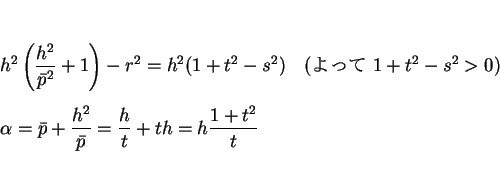
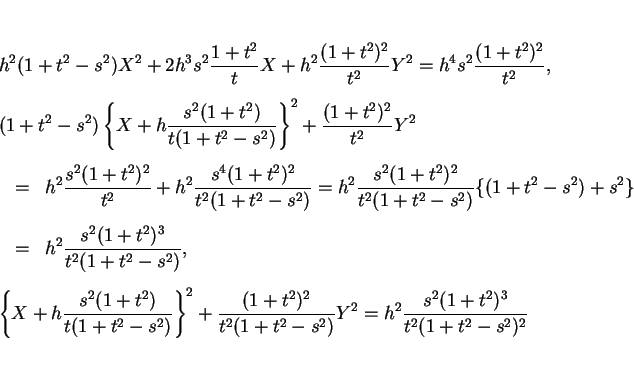
![]() 軸方向に
軸方向に ![]() 平行移動した場合に、
この楕円と光源である
平行移動した場合に、
この楕円と光源である
![]() が
が
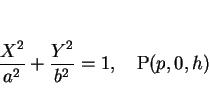
![]() が
が ![]() で
どのように表されるかが得られたことになるが、
逆に考えれば、
この
で
どのように表されるかが得られたことになるが、
逆に考えれば、
この ![]() の式 (10), (11), (12)
から
の式 (10), (11), (12)
から ![]() を消去して得られるのが、
元の図形が直円錐の一部となるための条件式、ということになる。
その条件式を以下で求める。
を消去して得られるのが、
元の図形が直円錐の一部となるための条件式、ということになる。
その条件式を以下で求める。