

Next: 10 最後に
Up: 斜円錐の側面積について
Previous: 8 根号内が完全平方になる場合
(PDF ファイル: yokoyama1.pdf)
9 数値計算結果
最後に、元の問題に対する数値計算結果を紹介する。
元々の問題には、
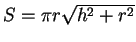 で求めて構わないか、
という要請も含まれているが、それに対する回答にもなっている。
なお、この節でも元々の問題の条件、
すなわち
で求めて構わないか、
という要請も含まれているが、それに対する回答にもなっている。
なお、この節でも元々の問題の条件、
すなわち 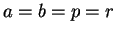 ,
, 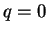 で考えることにする。
で考えることにする。
この場合、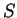 は 7 節で見たように
は 7 節で見たように
であり、この 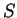 と直円錐の場合の側面積
と直円錐の場合の側面積
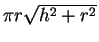 との比を考えて、その比 (
との比を考えて、その比 (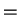 相対誤差) がどれくらいになるのかを見ることにする。
つまり、
相対誤差) がどれくらいになるのかを見ることにする。
つまり、
を 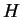 の関数
の関数 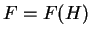 と見て、この値の増減を調べることにする。
容易に分かるように、
と見て、この値の増減を調べることにする。
容易に分かるように、
なので、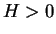 のどこかで最大値、または最小値を取ることはわかる。
しかし闇雲に数値計算するのも大変なので、
まずおおまかに
のどこかで最大値、または最小値を取ることはわかる。
しかし闇雲に数値計算するのも大変なので、
まずおおまかに 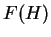 の増減を調べてみることにする。
微分と積分の順序交換の定理を使って
の増減を調べてみることにする。
微分と積分の順序交換の定理を使って 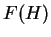 の導関数を計算する。
の導関数を計算する。
ここで、
となる。よって、
となるが、この後者の積分で
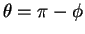 とすると、
とすると、
となる。この
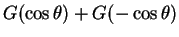 の符号を調べてみる。
の符号を調べてみる。
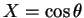 とすると、
とすると、
となるが、
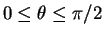 では
では 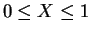 なので、
最後の式の前の方の分母と後ろの方の分数式全体は 0 以上、
よって、符号は前の方の分子の式で決まる。
これを展開すると、
なので、
最後の式の前の方の分母と後ろの方の分数式全体は 0 以上、
よって、符号は前の方の分子の式で決まる。
これを展開すると、
となる。よって、
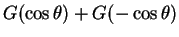 の符号は
の符号は
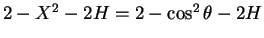 で決まることになるので、
で決まることになるので、
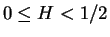 では
では
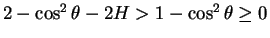 より
より
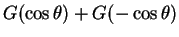 は常に正となるので
は常に正となるので 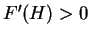 、
すなわちこの範囲では
、
すなわちこの範囲では 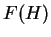 は増加、
は増加、
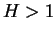 では
では
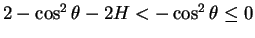 より
より
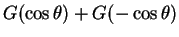 は常に負となるので
は常に負となるので 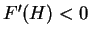 、
すなわちこの範囲では
、
すなわちこの範囲では 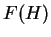 は減少
は減少
となる。よって、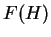 の増減は後は
の増減は後は
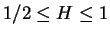 の値で決まることになり、
多分この区間内に
の値で決まることになり、
多分この区間内に 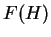 の最大値があると予想される。
つまりこの区間でだけ
の最大値があると予想される。
つまりこの区間でだけ 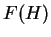 の値を調べてみれば良い。
の値を調べてみれば良い。
なお、元の出題者が必要としていた 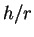 の値は
の値は
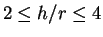 位で
あるらしいので、
位で
あるらしいので、
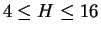 での最大値も必要となるが、
それは上の考察から
での最大値も必要となるが、
それは上の考察から 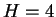 のときの値となる。
よって、
のときの値となる。
よって、
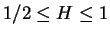 、および
、および 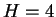 (ついでに
(ついでに 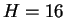 ) での
) での 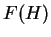 の
値を数値計算すればいいことになる。
の
値を数値計算すればいいことになる。
積分の数値計算には、良く用いられるシンプソンの公式を使用する。
シンプソンの公式は、
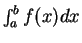 の積分を、
区間
の積分を、
区間 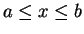 を
を 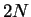 等分して、
等分して、
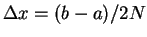 とするとき、
とするとき、
によって近似計算する方法である。これを 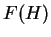 に用いる。
に用いる。
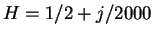 (
(
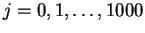 ) に対する
) に対する 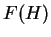 の値を、
の値を、
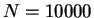 に対するシンプソンの公式を用いて数値計算して得た値を
グラフにしたのが図 8 である。
横軸が
に対するシンプソンの公式を用いて数値計算して得た値を
グラフにしたのが図 8 である。
横軸が 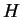 を、縦軸が
を、縦軸が 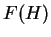 を表している。
を表している。
図 8:
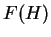 のグラフ (
のグラフ (
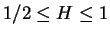 )
)
|
|
これを見て分かるように 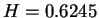 (
(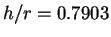 ) 付近で最大値約 1.0727 をとり、
その両側では単調になっている。
) 付近で最大値約 1.0727 をとり、
その両側では単調になっている。
また、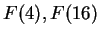 はそれぞれ
はそれぞれ 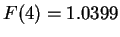 ,
, 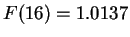 位であった。
結局、
位であった。
結局、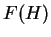 は
は
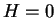 では
では 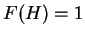 、
、
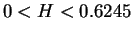 (
(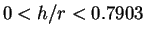 )
では
)
では 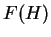 は増加、
は増加、
-
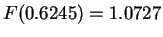 (
(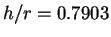 ) が最大値、
) が最大値、
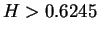 (
(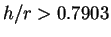 ) では
) では 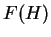 は減少
は減少
-
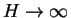 では
では 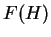 は 1 に収束
は 1 に収束
-
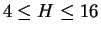 (
(
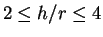 ) では
) では 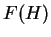 の最大値は
の最大値は
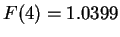
ということになる。
質問者に取っては相対誤差は 1.0399 位、
その範囲を越えても高々 1.0727 位になるわけであるが、
これくらいの値になると報告してみたところ、
他の要因のためにも少し余裕を見ているのでこれくらいの誤差なら全く問題はない、
ということであった。


Next: 10 最後に
Up: 斜円錐の側面積について
Previous: 8 根号内が完全平方になる場合
Shigeharu TAKENO
2005年 2月 28日
![]() は 7 節で見たように
は 7 節で見たように
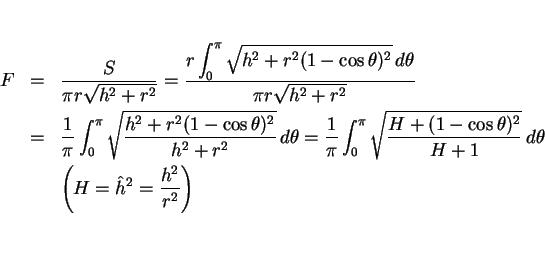
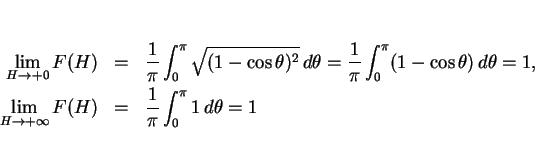
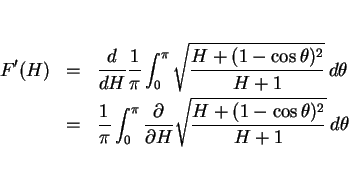
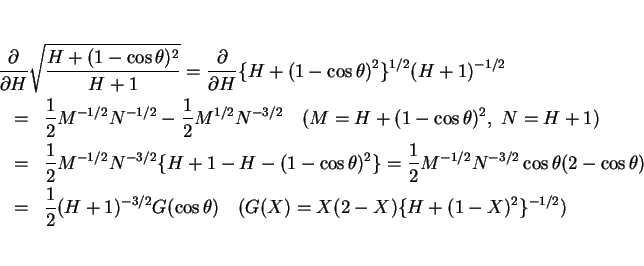
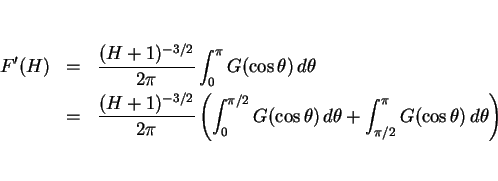
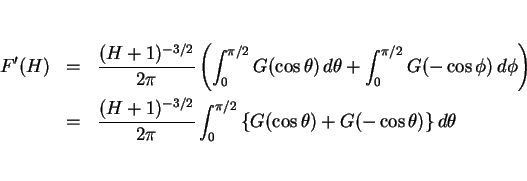
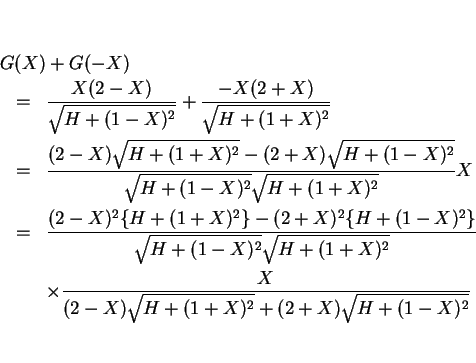
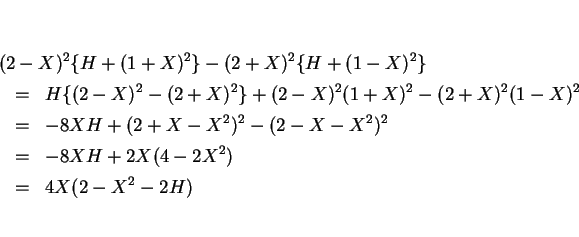
![]() の値は
の値は
![]() 位で
あるらしいので、
位で
あるらしいので、
![]() での最大値も必要となるが、
それは上の考察から
での最大値も必要となるが、
それは上の考察から ![]() のときの値となる。
よって、
のときの値となる。
よって、
![]() 、および
、および ![]() (ついでに
(ついでに ![]() ) での
) での ![]() の
値を数値計算すればいいことになる。
の
値を数値計算すればいいことになる。
![]() の積分を、
区間
の積分を、
区間 ![]() を
を ![]() 等分して、
等分して、
![]() とするとき、
とするとき、
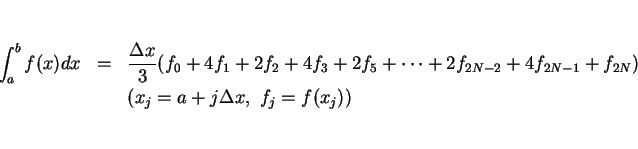
![]() (
(
![]() ) に対する
) に対する ![]() の値を、
の値を、
![]() に対するシンプソンの公式を用いて数値計算して得た値を
グラフにしたのが図 8 である。
横軸が
に対するシンプソンの公式を用いて数値計算して得た値を
グラフにしたのが図 8 である。
横軸が ![]() を、縦軸が
を、縦軸が ![]() を表している。
を表している。
![]() はそれぞれ
はそれぞれ ![]() ,
, ![]() 位であった。
結局、
位であった。
結局、![]() は
は