5 y3 の場合
次は、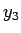 の場合を考えてみる。
の場合を考えてみる。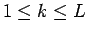 に対し (5) より、
に対し (5) より、
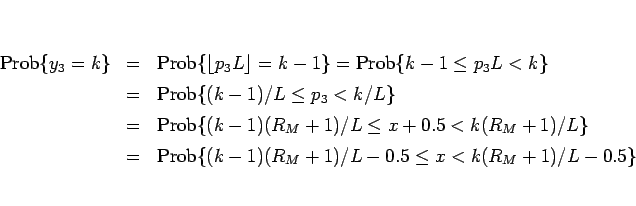
となるが、
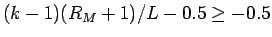 ,
,
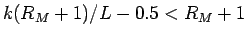 なので、やはり補題 1 により、
なので、やはり補題 1 により、
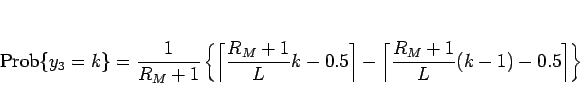
となる。よってこの分子を 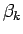 とすれば、
補題 2 により
この
とすれば、
補題 2 により
この 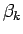 も (17) 同様
も (17) 同様
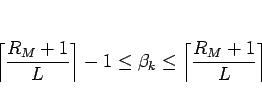
を満たすことがわかり、
よって 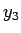 も最適な均等配分のひとつであることがわかる。
も最適な均等配分のひとつであることがわかる。
なお、
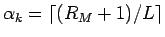 となる
となる 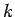 の個数と
の個数と
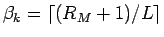 となる
となる 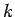 の個数は同じになるが、
そのような
の個数は同じになるが、
そのような 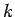 の集合自体が一致するわけではないので
(例えば
の集合自体が一致するわけではないので
(例えば 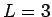 で考えよ)、
で考えよ)、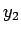 と
と 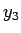 が一致するわけではない。
が一致するわけではない。
同様にすれば、一般に、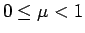 である実数定数
である実数定数 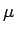 に対し、
に対し、
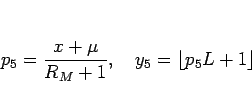 |
(18) |
も、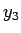 と同じ議論により、
と同じ議論により、
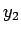 と同じく最良の均等配分になることがわかる。
と同じく最良の均等配分になることがわかる。
竹野茂治@新潟工科大学
2007年6月22日
![]() となる
となる ![]() の個数と
の個数と
![]() となる
となる ![]() の個数は同じになるが、
そのような
の個数は同じになるが、
そのような ![]() の集合自体が一致するわけではないので
(例えば
の集合自体が一致するわけではないので
(例えば ![]() で考えよ)、
で考えよ)、![]() と
と ![]() が一致するわけではない。
が一致するわけではない。
![]() である実数定数
である実数定数 ![]() に対し、
に対し、