3 μ=1 の場合
次に、方程式 (5) の 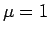 の場合
の場合
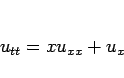 |
(8) |
に対して、[1] に基づいた手法 (変数分離法) で 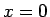 での境界条件 (6) の必要性について考察する。
での境界条件 (6) の必要性について考察する。
(8) の 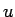 を
を 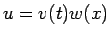 と変数分離すると、
と変数分離すると、
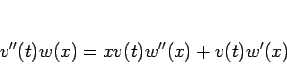
となるので、

と分離でき、これは 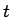 のみの式と
のみの式と 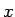 のみの式が等しいことを意味するので、
この両辺は定数となる。それを
のみの式が等しいことを意味するので、
この両辺は定数となる。それを 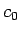 とする。
とする。
 であると、
であると、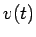 は限りなく増大するか、
または単調に減少する関数になってしまい、
それでは本来の糸の運動に対応する振動する解を表現できないので、
は限りなく増大するか、
または単調に減少する関数になってしまい、
それでは本来の糸の運動に対応する振動する解を表現できないので、
 である必要がある。
よって
である必要がある。
よって
 (
(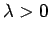 ) と書くことにすると、
) と書くことにすると、
| |
|
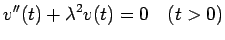 |
(9) |
| |
|
 |
(10) |
となる。(9) より 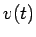 は
は
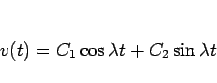
と求まるが、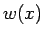 はベッセル関数で表されるものとなる。
はベッセル関数で表されるものとなる。
竹野茂治@新潟工科大学
2009年6月22日
![]() を
を ![]() と変数分離すると、
と変数分離すると、
![]() であると、
であると、![]() は限りなく増大するか、
または単調に減少する関数になってしまい、
それでは本来の糸の運動に対応する振動する解を表現できないので、
は限りなく増大するか、
または単調に減少する関数になってしまい、
それでは本来の糸の運動に対応する振動する解を表現できないので、
![]() である必要がある。
よって
である必要がある。
よって
![]() (
(![]() ) と書くことにすると、
) と書くことにすると、