1 はじめに
[1] の 13 章に、つり下げられた糸の自由振動として、
次のような方程式が書かれている (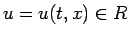 )。
)。
これは、横軸が 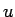 、縦軸が
、縦軸が 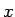 軸の
軸の 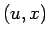 平面の、
平面の、
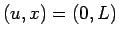 の位置から長さ
の位置から長さ 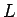 の糸をたらしたときの
糸の微小な振動の運動方程式で、
の糸をたらしたときの
糸の微小な振動の運動方程式で、
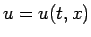 は、高さ
は、高さ 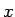 での糸の横方向の変位を表している。
での糸の横方向の変位を表している。
なお、元の [1] とは少し記号を変えているし、
また [1] には 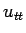 の前に定数がついているのであるが、
簡単のためここではそれは 1 とした。
の前に定数がついているのであるが、
簡単のためここではそれは 1 とした。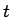 のスケール変換を行えば、
そのようにしてよいことは容易に確認できる。
のスケール変換を行えば、
そのようにしてよいことは容易に確認できる。
この方程式 (1) は 2 階の線形偏微分方程式で、
その主要部は
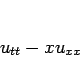 |
(4) |
であるから、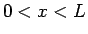 では双曲型の方程式であり、
よって通常なら (1) の方程式の境界条件 (3) はこれだけでは足りず、
もう一方の境界
では双曲型の方程式であり、
よって通常なら (1) の方程式の境界条件 (3) はこれだけでは足りず、
もう一方の境界 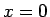 でも境界条件を 1 つ与える必要があるように見える (2 節参照)。
でも境界条件を 1 つ与える必要があるように見える (2 節参照)。
しかし、境界 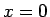 はこの方程式の特性方向になっていて (特性境界)、
しかも
はこの方程式の特性方向になっていて (特性境界)、
しかも 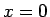 では双曲性が退化しているので、
通常の双曲型方程式とは状況はだいぶ異なる。
では双曲性が退化しているので、
通常の双曲型方程式とは状況はだいぶ異なる。
本稿では、(1) をやや一般化した方程式
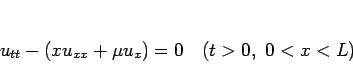 |
(5) |
に対して、
その境界条件が (3) で足りるのか、
それとも 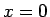 での境界条件
での境界条件
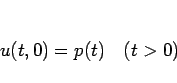 |
(6) |
も必要であるのかについて、
[1] の手法、及び数値計算によって考察する。
(1) は (5) の 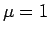 の場合になっているが、
それについては 3 節、5 節で考察する。
の場合になっているが、
それについては 3 節、5 節で考察する。
竹野茂治@新潟工科大学
2009年6月22日
![]() の前に定数がついているのであるが、
簡単のためここではそれは 1 とした。
の前に定数がついているのであるが、
簡単のためここではそれは 1 とした。![]() のスケール変換を行えば、
そのようにしてよいことは容易に確認できる。
のスケール変換を行えば、
そのようにしてよいことは容易に確認できる。
![]() はこの方程式の特性方向になっていて (特性境界)、
しかも
はこの方程式の特性方向になっていて (特性境界)、
しかも ![]() では双曲性が退化しているので、
通常の双曲型方程式とは状況はだいぶ異なる。
では双曲性が退化しているので、
通常の双曲型方程式とは状況はだいぶ異なる。