4 ベッセル関数
ベッセル関数は、
例えば [1], [2], [3], [4], [5] などに詳しく書かれているが、ここではその概要を述べる。
詳しくはそれらを参照のこと。
ベッセル関数は、次のベッセルの微分方程式を満たす関数である (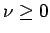 は定数)。
は定数)。
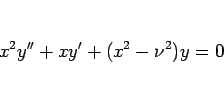 |
(11) |
この (11) は 2 階の線形微分方程式であるから、
2 つの一次独立な解 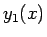 ,
, 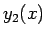 を持ち、その一般解は
を持ち、その一般解は
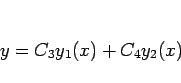
と書ける。その 1 つの解が 第 1 種ベッセル関数 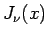
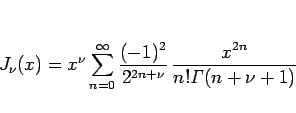 |
(12) |
であり、(12) の 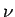 の代わりに
の代わりに 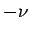 とした
とした 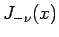 も (11) の解となる。
も (11) の解となる。
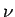 が整数でなければ
が整数でなければ 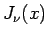 と
と 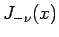 は
一次独立であるが、
は
一次独立であるが、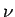 が整数
が整数 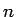 である場合は、
である場合は、
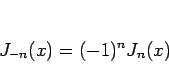
となってしまうため、この 2 つは一次独立にならない。
そのため、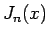 に一次独立なもう 1 つの解を得るために、
以下のように定義される 第 2 種ベッセル関数 (又は ノイマン関数 と呼ばれる)
に一次独立なもう 1 つの解を得るために、
以下のように定義される 第 2 種ベッセル関数 (又は ノイマン関数 と呼ばれる) 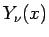 が導入される。
が導入される。
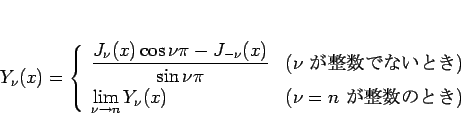
この 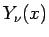 は、
は、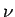 が整数であろうとなかろうと
が整数であろうとなかろうと 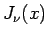 とは一次独立になるので、
よって
とは一次独立になるので、
よって 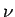 が整数でないときは、
が整数でないときは、
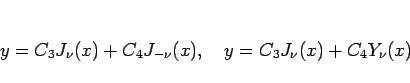
のいずれも (11) の一般解であり、
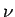 が整数
が整数 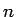 のときは、
のときは、
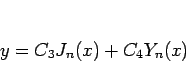
が (11) の一般解となる。
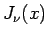 は、(12) からもわかるが、
は、(12) からもわかるが、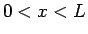 では有界な関数で、
では有界な関数で、
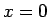 の付近では
の付近では
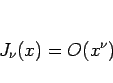 |
(13) |
となっている。一方、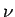 が整数でない場合の
が整数でない場合の 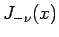 は、
は、
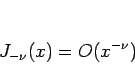 |
(14) |
となる。そして、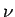 が整数
が整数 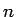 の場合の
の場合の 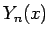 は、
は、
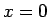 の近くでは有界ではなく、
の近くでは有界ではなく、
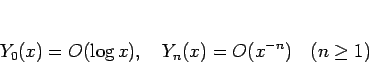 |
(15) |
であることが知られている。
ベッセル関数 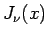 は、
は、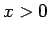 に無限個の離散的な零点
に無限個の離散的な零点
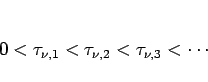 |
(16) |
を持つことが知られていて、
この零点に関して次のような直交性が成り立つことが知られている。
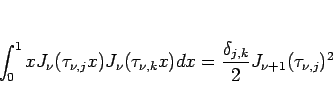
ここで、
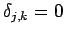 (
(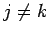 ),
),
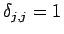 である。
そして、この直交性により
である。
そして、この直交性により 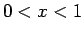 上の関数
上の関数 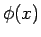 を、
を、
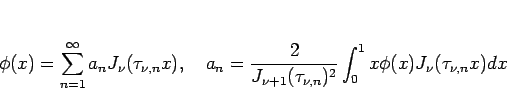 |
(17) |
のようにベッセル関数により級数展開できる (フーリエ・ベッセル展開 と呼ばれる) が、
その展開の完全性、すなわちすべての関数をこのように
表すことができるかどうかについては、
[5] のベッセル関数の項にその結果のみ紹介されている (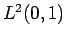 での完全性)。
での完全性)。
竹野茂治@新潟工科大学
2009年6月22日
![]() は定数)。
は定数)。
![]() が整数でなければ
が整数でなければ ![]() と
と ![]() は
一次独立であるが、
は
一次独立であるが、![]() が整数
が整数 ![]() である場合は、
である場合は、
![]() は、(12) からもわかるが、
は、(12) からもわかるが、![]() では有界な関数で、
では有界な関数で、
![]() の付近では
の付近では
![]() は、
は、![]() に無限個の離散的な零点
に無限個の離散的な零点