3 死を考慮したフィボナッチ数列
本節では、2 節で考察した問題を、
「有限期間で死ぬ」などを考慮したものに変えて考えてみる。
- 設定 1. うさぎは、生後
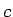 ヶ月後に死ぬものとする
ヶ月後に死ぬものとする
(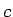 は 1 以上の整数、通常のフィボナッチ数列では
は 1 以上の整数、通常のフィボナッチ数列では 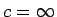 )
)
- 設定 2. うさぎのつがいは生後
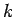 ヶ月目から
ヶ月目から 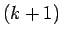 ヶ月目までの間、すなわち月齢
ヶ月目までの間、すなわち月齢 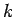 月の間に
月の間に 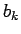 つがいの
うさぎを産むとする (
つがいの
うさぎを産むとする (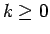 )
)
(通常のフィボナッチ数列では、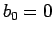 、
、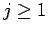 に対し
に対し 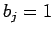 )
)
今、通常のフィボナッチ数列と同様に最初は産まれたての 1 つがいから始めて、
開始から 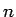 ヶ月後に月齢
ヶ月後に月齢 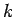 月 (
月 (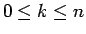 ) のつがいの数を
) のつがいの数を
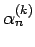 と書くことにすると、上記の設定により次が成り立つ。
と書くことにすると、上記の設定により次が成り立つ。
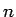 ヶ月後のつがいの総数
ヶ月後のつがいの総数 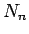 は、
は、
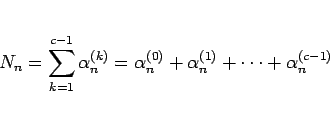 |
(17) |
であるが、それが満たす漸化式を考えてみる。
まず、(14) を用いると、
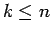 の場合の
の場合の
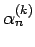 は
は
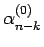 に等しく、
2 重添字を必要としない
に等しく、
2 重添字を必要としない
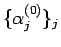 で表せる。
また、(14), (16) を用いて
で表せる。
また、(14), (16) を用いて
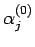 を
を 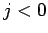 に対しても拡張すると、
に対しても拡張すると、
より、結局
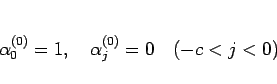 |
(18) |
と定めればよいことになる。
そしてこれにより、上の関係式はすべて
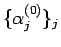 で
表せることになる。例えば、(15) は、
で
表せることになる。例えば、(15) は、
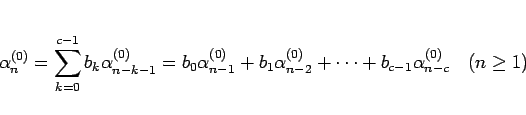 |
(19) |
となり、(17) の総数 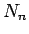 は、
は、
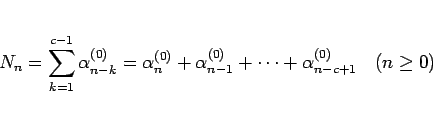 |
(20) |
となる。
これにより、数列
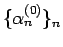 は、
は、
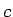 個の値 (18) を初期値とし、
個の値 (18) を初期値とし、
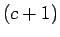 階の線形漸化式 (19) によって決まる数列、
と見ることができる。
階の線形漸化式 (19) によって決まる数列、
と見ることができる。
なお、(14) より
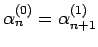 であるから、
(19) より
であるから、
(19) より
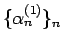 に関する漸化式
に関する漸化式
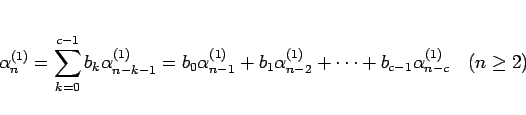 |
(21) |
が成り立つことがわかる。
これは、(19) と同形の漸化式であるが、
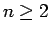 である必要がある。同様にして、
である必要がある。同様にして、
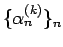 (
(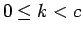 ) は、
) は、
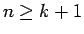 に対して、同形の漸化式を満たすこともわかる。
に対して、同形の漸化式を満たすこともわかる。
さらに、(20) の右辺のすべての項に
(19) を代入して、各 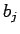 でまとめると、
でまとめると、
となり、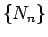 も同形の漸化式を満たすことがわかる。
なお、(22) が成立する
も同形の漸化式を満たすことがわかる。
なお、(22) が成立する 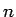 は、
(19) が
は、
(19) が 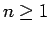 で成り立ち、
(20) が
で成り立ち、
(20) が 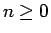 で成り立つので、
(22) は
で成り立つので、
(22) は 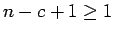 、
すなわち
、
すなわち 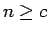 で成り立つことになる。
これが、死を考慮したフィボナッチ数列となる。
で成り立つことになる。
これが、死を考慮したフィボナッチ数列となる。
今、例えば 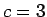 ,
, 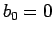 ,
, 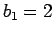 ,
, 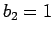 としたものを考えてみる。
この場合、漸化式 (22) は
としたものを考えてみる。
この場合、漸化式 (22) は
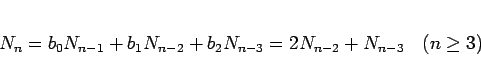 |
(23) |
となる。初期値は、
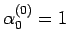 ,
,
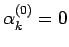 (
(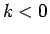 ) で、
(19) より
) で、
(19) より
なので、(20) より
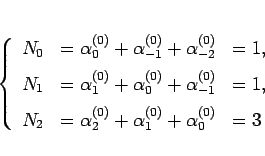 |
(24) |
となる。この (23), (24) より 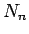 が決定する。
が決定する。
(23) の特性方程式とその解は、
となるので、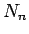 は、
は、
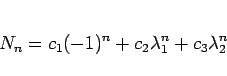 |
(25) |
となる。後半 2 項は、フィボナッチ数列の一般解になっている。
実は、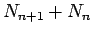 は、(23) より
は、(23) より
となるからフィボナッチ数列と同じ漸化式を満たし、
より
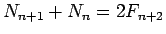 となることがわかる。
となることがわかる。
さて、(25) の 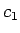 ,
, 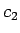 ,
, 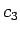 は、
初期値 (24) を
元に連立方程式を解くと
は、
初期値 (24) を
元に連立方程式を解くと 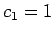 ,
,
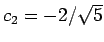 ,
,
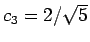 と
求まる。よって、
と
求まる。よって、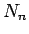 の一般項は
の一般項は
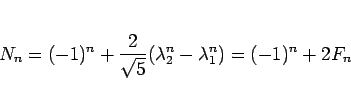 |
(26) |
となることがわかる。
または、上で示した
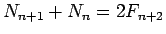 より (26) を導くこともできる。
それも紹介しよう。
まずこの関係式より、
より (26) を導くこともできる。
それも紹介しよう。
まずこの関係式より、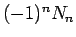 の階差数列が
の階差数列が
となり、よって、
がわかる。一方、フィボナッチ数列の漸化式 (1) を
上と同様に 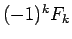 の階差数列の形に変形して、
の階差数列の形に変形して、
とすれば、
がわかる。なお、上の計算は 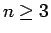 で成り立つが、
結果は
で成り立つが、
結果は 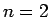 でも成り立つことに注意する。
よって、(27), (28) より、
でも成り立つことに注意する。
よって、(27), (28) より、
となり、この両辺を 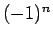 で割れば (26) が得られる。
で割れば (26) が得られる。
さて、(26) より結果的にこの 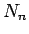 は、
フィボナッチ数列の 2 倍と 1 しか違わない値で、
死を考慮に入れたモデルでも増え方はそれほど変わっていないことになる。
は、
フィボナッチ数列の 2 倍と 1 しか違わない値で、
死を考慮に入れたモデルでも増え方はそれほど変わっていないことになる。
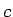 や
や 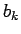 の設定を変えれば数列は変わるが、
(22) は定数係数線形の漸化式なので、
その一般解は基本的には特性方程式の解の巾乗の和のようなもので
表され、やはりこの例と似た形になる。
の設定を変えれば数列は変わるが、
(22) は定数係数線形の漸化式なので、
その一般解は基本的には特性方程式の解の巾乗の和のようなもので
表され、やはりこの例と似た形になる。
しかし、特性方程式の解は 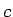 や
や 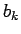 などの値によって
絶対値が 1 より小さくなる場合もあるし、虚数解を持つ場合もありうる。
そのような 1 例を紹介する。
なお、元の問題の設定では
などの値によって
絶対値が 1 より小さくなる場合もあるし、虚数解を持つ場合もありうる。
そのような 1 例を紹介する。
なお、元の問題の設定では 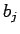 は 0 以上の整数を
考えるのが自然かもしれないが、
元の個体数が多く、産む数を「1 つがい当たりの平均値」と考えれば、
は 0 以上の整数を
考えるのが自然かもしれないが、
元の個体数が多く、産む数を「1 つがい当たりの平均値」と考えれば、
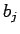 の値は必ずしも整数である必要はない。
の値は必ずしも整数である必要はない。
例えば、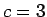 ,
, 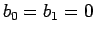 ,
, 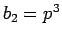 (
(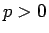 ) とすると、
) とすると、
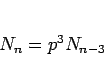 |
(29) |
で、これは生まれて 2 月目までは何も産まず、3 ヶ月目に死ぬ直前に
まとめて 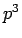 つがい産む、というモデルで、13 年ゼミ、
17 年ゼミのように長い間地中でさなぎとして過ごす生物の生態に近い。
つがい産む、というモデルで、13 年ゼミ、
17 年ゼミのように長い間地中でさなぎとして過ごす生物の生態に近い。
この場合特性方程式は 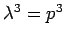 であるから、
であるから、
であり、よって一般項は
となる。
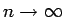 のとき、この
のとき、この 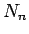 は
は 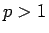 なら発散し、
なら発散し、
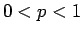 なら 0 に収束する (絶滅)。
なら 0 に収束する (絶滅)。
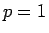 、すなわち 1 つがいから平均的に 1 つがい分しか生まれない場合は
、すなわち 1 つがいから平均的に 1 つがい分しか生まれない場合は
なので、周期的な増減を繰り返す (周期は 3)。
竹野茂治@新潟工科大学
2017年3月22日
![]() の場合の
の場合の
![]() は
は
![]() に等しく、
2 重添字を必要としない
に等しく、
2 重添字を必要としない
![]() で表せる。
また、(14), (16) を用いて
で表せる。
また、(14), (16) を用いて
![]() を
を ![]() に対しても拡張すると、
に対しても拡張すると、
![]() は、
は、
![]() 個の値 (18) を初期値とし、
個の値 (18) を初期値とし、
![]() 階の線形漸化式 (19) によって決まる数列、
と見ることができる。
階の線形漸化式 (19) によって決まる数列、
と見ることができる。
![]() であるから、
(19) より
であるから、
(19) より
![]() に関する漸化式
に関する漸化式
![]() でまとめると、
でまとめると、
![]() ,
, ![]() ,
, ![]() ,
, ![]() としたものを考えてみる。
この場合、漸化式 (22) は
としたものを考えてみる。
この場合、漸化式 (22) は
![]() ,
, ![]() ,
, ![]() は、
初期値 (24) を
元に連立方程式を解くと
は、
初期値 (24) を
元に連立方程式を解くと ![]() ,
,
![]() ,
,
![]() と
求まる。よって、
と
求まる。よって、![]() の一般項は
の一般項は
![]() より (26) を導くこともできる。
それも紹介しよう。
まずこの関係式より、
より (26) を導くこともできる。
それも紹介しよう。
まずこの関係式より、![]() の階差数列が
の階差数列が
![]() は、
フィボナッチ数列の 2 倍と 1 しか違わない値で、
死を考慮に入れたモデルでも増え方はそれほど変わっていないことになる。
は、
フィボナッチ数列の 2 倍と 1 しか違わない値で、
死を考慮に入れたモデルでも増え方はそれほど変わっていないことになる。
![]() や
や ![]() の設定を変えれば数列は変わるが、
(22) は定数係数線形の漸化式なので、
その一般解は基本的には特性方程式の解の巾乗の和のようなもので
表され、やはりこの例と似た形になる。
の設定を変えれば数列は変わるが、
(22) は定数係数線形の漸化式なので、
その一般解は基本的には特性方程式の解の巾乗の和のようなもので
表され、やはりこの例と似た形になる。
![]() や
や ![]() などの値によって
絶対値が 1 より小さくなる場合もあるし、虚数解を持つ場合もありうる。
そのような 1 例を紹介する。
なお、元の問題の設定では
などの値によって
絶対値が 1 より小さくなる場合もあるし、虚数解を持つ場合もありうる。
そのような 1 例を紹介する。
なお、元の問題の設定では ![]() は 0 以上の整数を
考えるのが自然かもしれないが、
元の個体数が多く、産む数を「1 つがい当たりの平均値」と考えれば、
は 0 以上の整数を
考えるのが自然かもしれないが、
元の個体数が多く、産む数を「1 つがい当たりの平均値」と考えれば、
![]() の値は必ずしも整数である必要はない。
の値は必ずしも整数である必要はない。
![]() ,
, ![]() ,
, ![]() (
(![]() ) とすると、
) とすると、
![]() であるから、
であるから、